动态WRR算法(权重轮询)

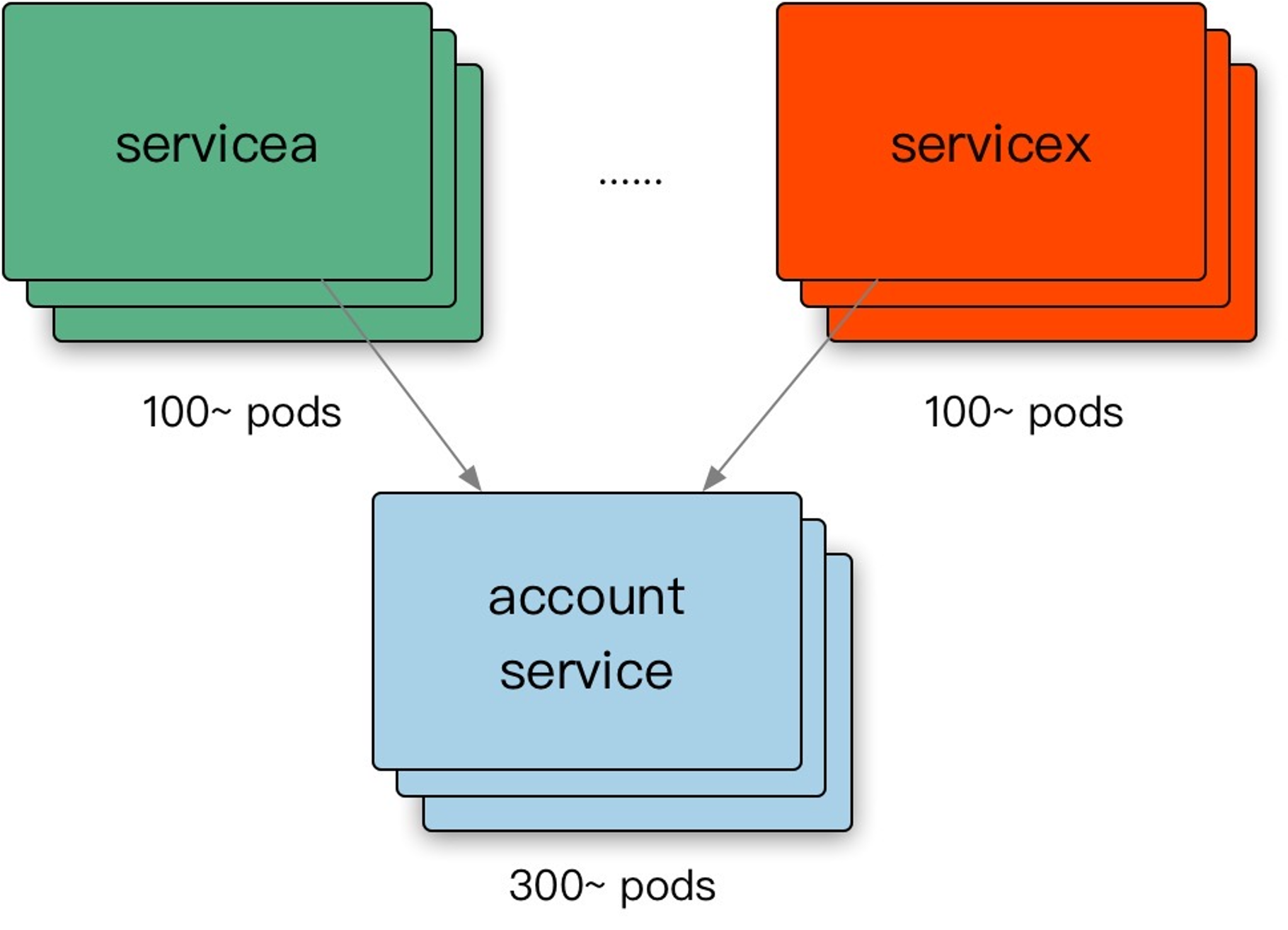
数据中心内部的负载均衡

在理想情况下，某个服务的负载会完全均匀地分发给所有的后端任务。在任何时刻，最忙和最不忙的节点永远消耗同样数量的CPU。

目标：

  • 均衡的流量分发。
  • 可靠的识别异常节点。
  • scale-out，增加同质节点扩容。
  • 减少错误，提高可用性。

我们发现在 backend 之间的 load 差异比较大：

  • 每个请求的处理成本不同。

  • 物理机环境的差异:

    • 服务器很难强同质性。
    • 存在共享资源争用（内存缓存、带宽、IO等）。

  • 性能因素:

    • FullGC。
    • JVM JIT。

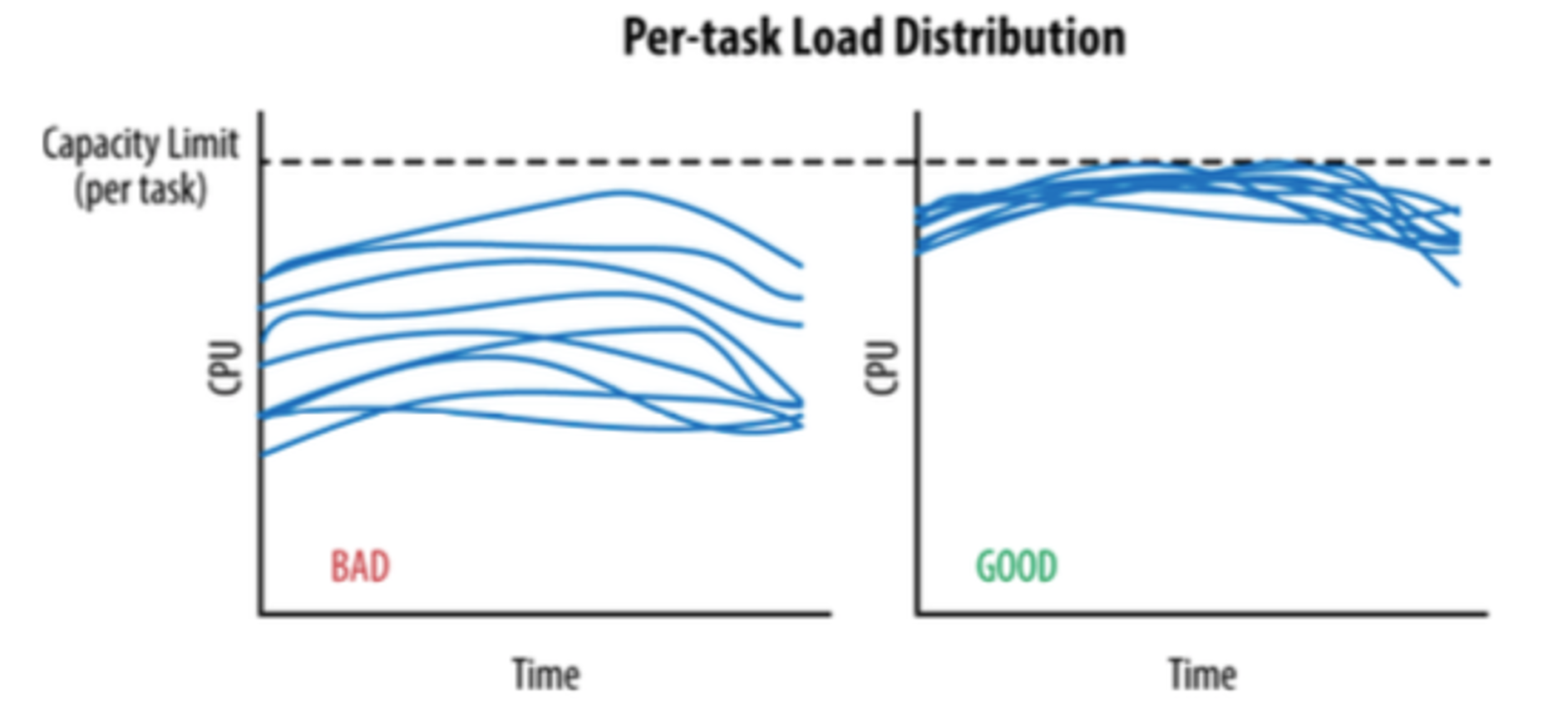
参考JSQ（最闲轮训）负载均衡算法带来的问题，缺乏的是服务端全局视图，因此我们目标需要综合考虑：负载+可用性。

Kratos 在传统的 Nginx-WRR 算法 的基础上，为加权轮询算法增加了 动态调节权重值 ，用户可以在为每一个 Backend 先配置一个初始的权重分，之后算法会根据 Backend 节点 CPU、延迟、服务端错误率、客户端错误率动态打分，（每一次 RPC 调用后）在将打分乘用户自定义的初始权重分得到最后的权重值。

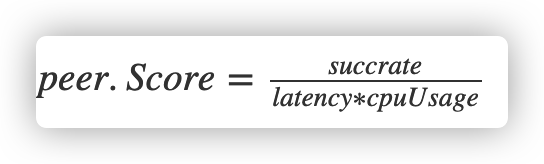
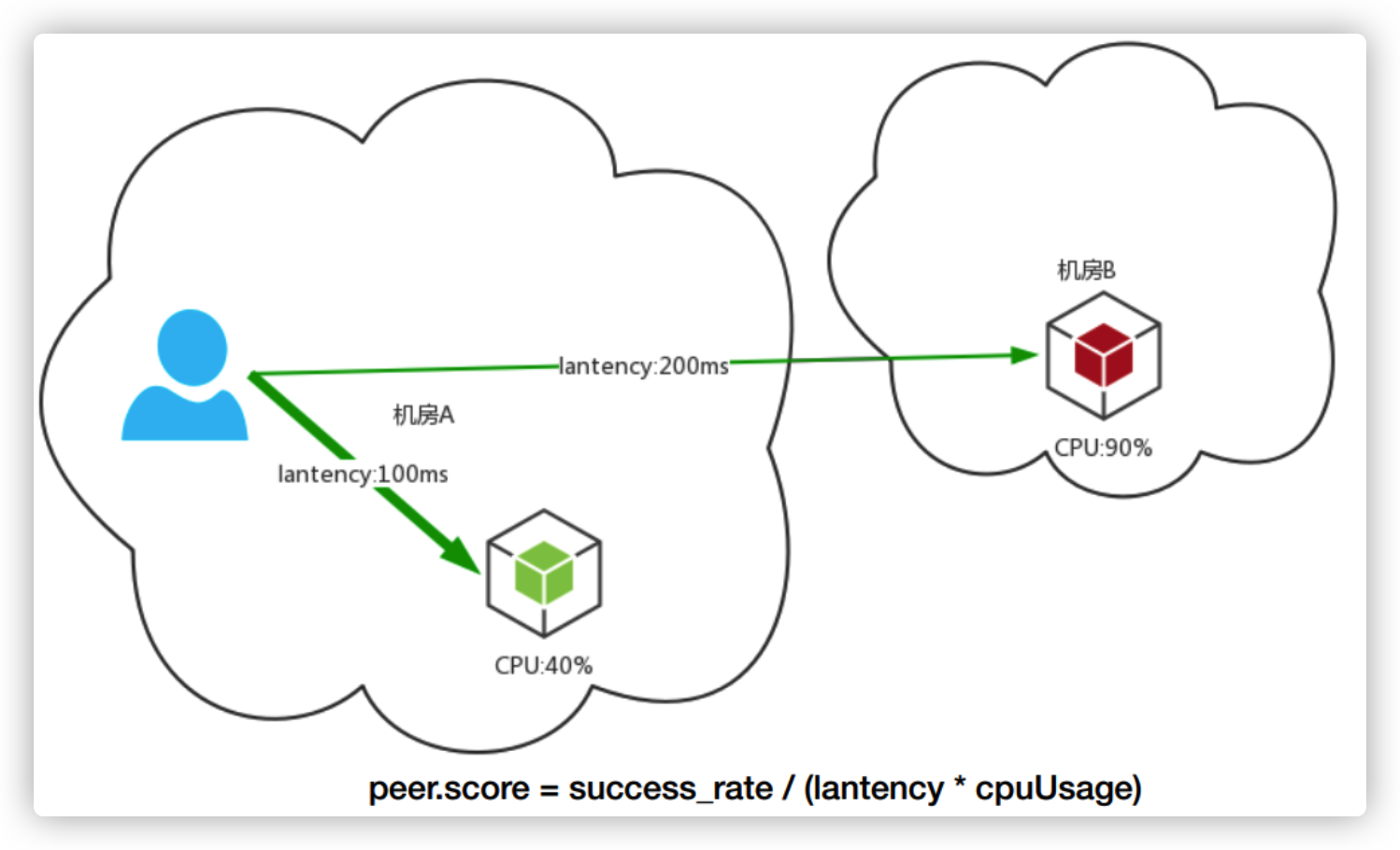
动态感知的 WRR 算法，利用每次 RPC 请求返回的 Response 夹带 CPU 使用率，尽可能感知到服务负载，并且每隔一段时间整体调整一次节点的权重分数，虽然解决了原生WRR的权重固定的问题，但是存在羊群效应问题：“发现其实是信息滞后和分布式带来的羊群效应”，即

就是WRR版本的负载均衡算法虽然会自动刷新权重值，但是在刷新时无法做到完全的实时，再快也不可能超过一个 RTT，都会存在一些信息延迟差。当后台资源比较稀缺时，遇到网络抖动时，就可能会把该节点炸掉，但是在监控上面是感觉不到的，因为 CPU 已经被平均掉了。

从上面的描述看，问题的本质在于gRPC的负载均衡是在客户端实现的，客户端每次请求完获取到服务端CPU数据，可能会存在延迟，在延迟的空档期，大量请求涌入，导致某个后端Node接收大量请求，从而不可用的问题。

P2C算法

介绍

常见的Load balance算法想必大家都不陌生，Random、Round-robin、Least connection、Consistent hash等应该都耳熟能详，这些算法都在实践中有广泛的应用，例如Nginx、Haproxy等负载均衡模块都有相应算法的实现。本文将和大家分享一种全新的Load balance算法：Power of Two Random Choices，也算是Fast 2019 best paper解读《Distcache: Provable load balancing for large-scale storage systems with distributed caching》 的续篇，DistCache利用Power of two random choices实现Cache Query的Load balance：就是在查询Cache中item的时候，从命中的2个Cache节点中选择负载较低的Cache节点来服务；实现简单，效果却不简单。除此之外，新版本的Nginx和Haproxy最近都增加了对Power of Two Random Choices算法的支持，可见一斑。

本文将从Power of Two Random Choices算法的起源说起（也就是数学里面经典的Balls into Bins问题），向大家展示Power of Two Random Choices算法背后的数学原理。并介绍其在解决Hash冲突中的应用，想必能进一步加深大家对Cuckoo Hash、BloomFilter等使用多个hash function做法的理解。

Balls into Bins

首先看数学一个经典的Balls into Bins问题：

假如顺序地将n个Balls投入到ｎ个bins（垃圾桶），策略是从n个bin中随机独立均匀地选择任意一个bin

那么当抛球结束的时候，以非常高的概率（ 也就是以概率1-ｏ(1)），n个bin中最大负载为(1+ｏ(1))logn/loglogn个balls。注意o(1)指的是高阶无穷小，可以直接忽略掉。

这实际上就是一个无状态的Load balance问题，考虑一个负载均衡器（LB）将n个请求随机等概率的发送给n个Server，那么就可以知道Server上最大的可能负载会是多少。

Power of two random choices

如果选择上做一个小改动，也就是今天要说的Power of two random choices：

假如顺序地将n个Balls投入到ｎ个bins（垃圾桶），策略是从n个bin中随机独立均匀地选择d个bin，然后选择Ball最少的bin放入

那么当抛球结束的时候，将以非常高的概率（ 也就是以概率1-ｏ(1)），n个bin中最大负载为(1+ｏ(1))loglogn/logd+Ｏ(1)个balls。

现在情况Balls的数量往往远大于Bins的数量，所以扩展一下：

假如顺序地将m个Balls投入到ｎ个bins（垃圾桶），策略是从n个bin中随机独立均匀地选择d个bin，然后选择Ball最少的bin放入，其中m>=n，d>=2

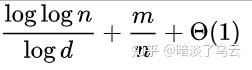
下面给出一个一组计算的算例，分别m=n={2^2,2^3,2^4……,2^64}，其中红色为普通的Balls into Bins问题的最大负载，蓝色为Power of two random choices d=2情况下的最大负载：

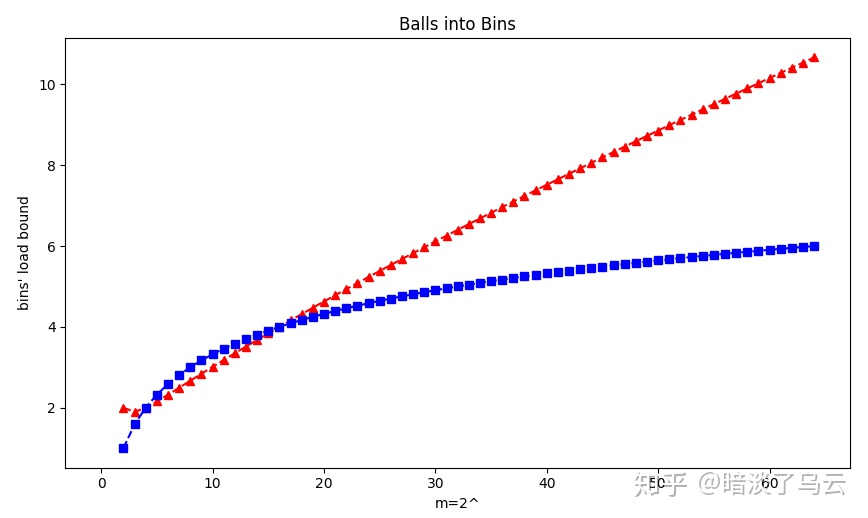
通过上图可以发现，Power of two random choices负载均衡的效果是不错的。尽管上面的模型太过理想，假定了所有的key都是必须均匀分布，每个request的size都是相同，和实际生产环境相差巨大，但仍然不妨碍我们认定这种做法的有效性。

伪代码

从可用后端节点列表中做 2 次选择操作（随机算法 or 依据一定策略来选择），得到节点 nodeA、nodeB 比较 nodeA、nodeB 两个节点，选出负载最低（一般是正在处理的连接数 / 请求数最少）的节点作为被选中的节点 伪代码如下：

1
2
3

nodeA = random_choice(nodes)
nodeB = random_choice(nodes)
best = least_connection_choice([nodeA, nodeB])

EWMA算法

加权移动平均算法

指数加权移动平均算法，是对观察值分别给予不同的权数，按不同权数求得移动平均值，并以最后的移动平均值为基础，确定预测值的方法。采用这种算法，是因为观察期的近期观察值对预测值有较大影响，它更能反映近期变化的趋势。

指数移动加权平均法，是指各数值的加权系数随时间呈指数式递减，越靠近当前时刻的数值加权系数就越大。

  1. 相较于普通的计算平均值算法，EWMA 不需要保存过去所有的数值，计算量显著减少，同时也减小了存储资源。
  2. 传统的计算平均值算法对网络耗时不敏感, 而 EWMA 可以通过请求频繁来调节 β，进而迅速监控到网络毛刺或更多的体现整体平均值。
    • 当请求较为频繁时, 说明节点网络负载升高了, 我们想监测到此时节点处理请求的耗时(侧面反映了节点的负载情况), 我们就相应的调小β。β越小，EWMA值 就越接近本次耗时，进而迅速监测到网络毛刺;
    • 当请求较为不频繁时, 我们就相对的调大β值。这样计算出来的 EWMA值 越接近平均值

公式如下：

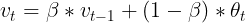
解释：vt代表第t次请求的指数加权平均耗时，vt-1代表上次请求的指数加权平均耗时，θt代表第t次请求的实际耗时。

β值的定义如下：

vt ≈ 1/(1 - β) 次的平均耗时

例：假设β等于0.9，1/(1 - β) 就等于10，也就是vt约等于它前10次请求的平均耗时；假设把β值调大道接近1，例如，将β等于0.98，1/(1-β)=50，按照刚刚的说法也就是当前请求的前50次请求的平均耗时。

由此可以推导出：

β值越大，统计区间越大，当前平均值的计算受到之前平均值的影响也就越大（曲线越平滑，呈现一个平缓的变化趋势）

β值越小，统计区间越小，当前平均值的计算受到之前平均值的影响也就越小（曲线贴近统计原值）

β极小时，便可以认为当次的平均耗时约等于当次本身的实际耗时。

上面的结论接下来会通过实验来进行验证。

其实这些根据上面的公式很容易推到出来，比如现在有两次请求，第一次耗时25ms，第二次耗时50ms，代入公式，计算出第一次和第二次的指数加权平均值为：

v1 = β 0 + (1 - β) 25

v2 = β v1 + (1 - β) 50

可以看到，β值越小，意味着本次请求的实际耗时占比越大，β值越大，之前计算得到的平均值占比越大。

根据上面的理解，相比普通平均值的计算，它更在乎的是一段时间内的平均趋势，而不是直接把当前实际耗时累加到总耗时里参与算术平均运算，这样有一个好处，那就是平均数变化会更加平滑（这个取决于β值的大小，后续会给出证明）。

我们再来利用此算法来模拟下1000次请求（同样为了模拟真实情况，让一些请求耗时过高），β我们取值0.9，代表最新请求时的平均值计算会受到最近10次耗时的影响进行平滑过渡，运行结果绘制如下图：

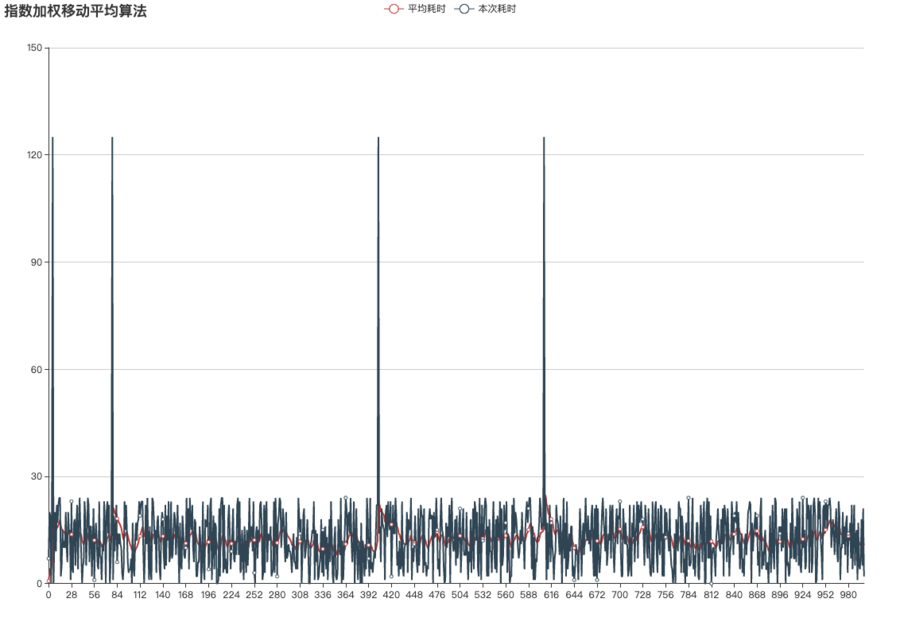
可以看到它得出的平均数曲线并没有算术平均那么稳定，但可以看出，每次网络波动会提升其加权均值，不像算术平均值那样完全不受网络波动影响。

接下来同样假设第100~200次请求，发生了网络延迟，延时5倍，再次利用ewma算法做下模拟：

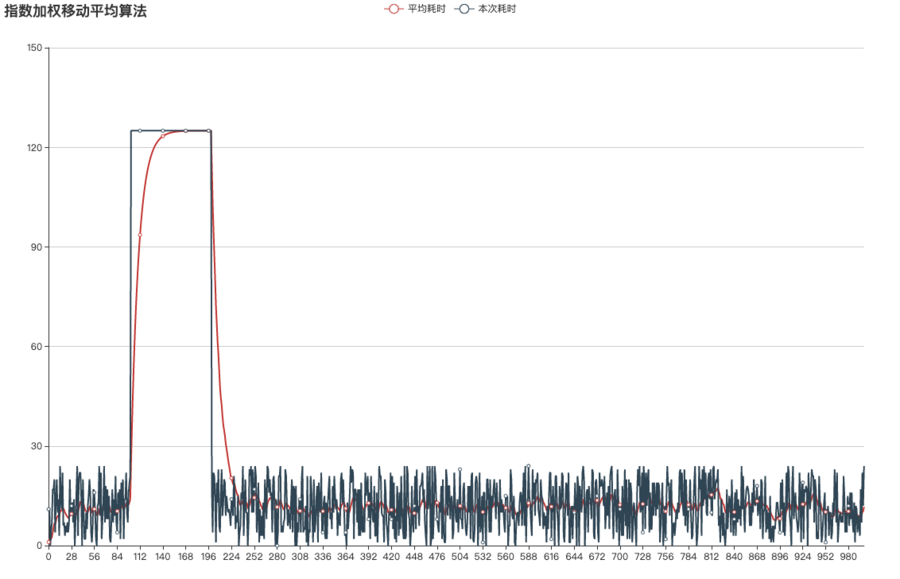
请将这张图跟图7进行对比，你会发现，利用指数加权平均算法计算出的平均值在网络恢复时，以极快的速度恢复到了正常水平。

相比算术平均的绝对平均值，指数加权移动平均算法更重要的是它平滑的模拟了平均值的趋势，平均值曲线的峰值和负峰值受β影响，β越大，则当前平均数受到前面数据的影响越大，反之越小，比如我们把图9里的β值调整为0.98，此时在计算当前平均值时则受到前面(1/0.02) = 50个平均值的影响，便得到下图：

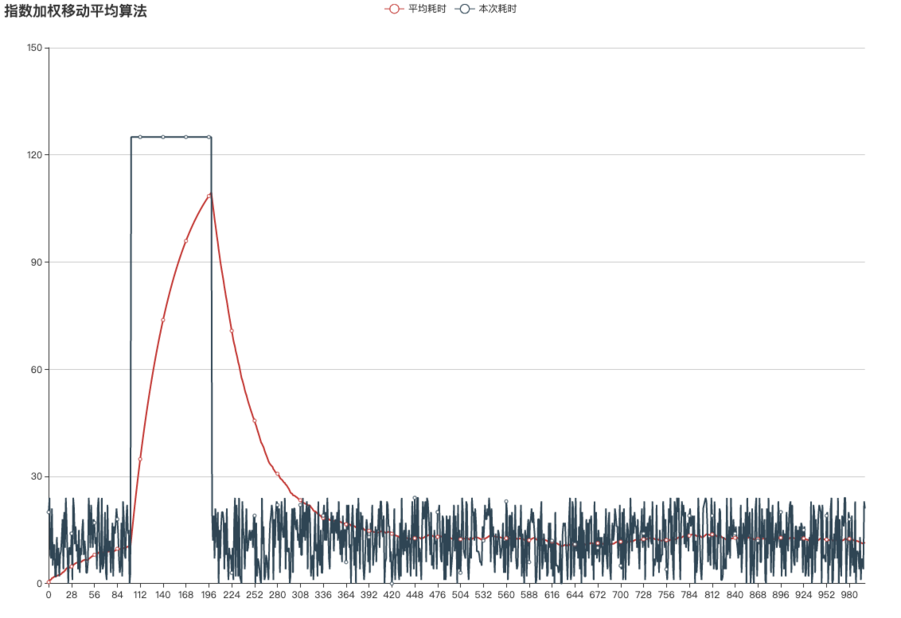
因为β值大，所以后续每个平均值都会受到更多前面值的影响，而自己的部分仅占很少影响（参考公式理解），所以它相比图9，在出现网络抖动后，更缓慢的恢复为正常均值，但由于它所统计的范围更大，因此平均数曲线会非常平缓，β值越大，统计周期越长，越能体现某个时段的平均趋势（比如图10里的平均数曲线已经趋近于算术平均数）。

再比如，我们将β设置为0.32，那么计算均值时仅受到前面(1/0.68) = 1.47个均值影响，说白了就是平均值轨迹几乎和正常响应时间重叠：

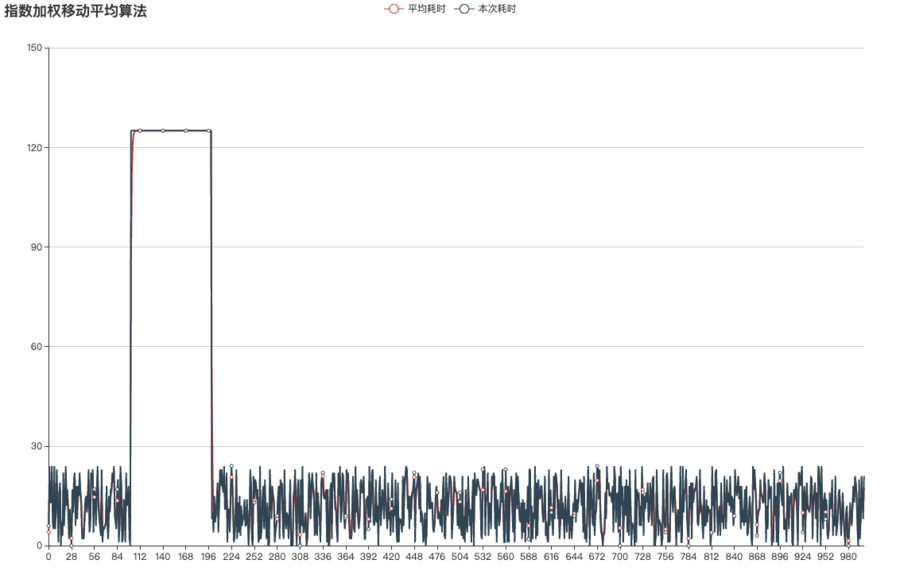
可以看到，当β很小时，受影响因子无限趋近于1，越趋近于1则越贴近原本值。

实验组 对照组 目的 结论
图6 图8（β=0.9） 模拟网络正常情况下，两种算法对均值的统计区别 算术平均值非常稳定，对单次网络抖动完全无感知，ewma均值则会随着响应时间动态变化，因此单次网络抖动后会稍微提升均值，之后便很快恢复
图7 图9（β=0.9） 模拟一段网络延迟，看两种算法的均值变化 算术平均值会缓慢提升，之后再次以极慢的速度下降，对网络延迟反映迟钝，网络延迟结束后仍然要花很长时间才能恢复到正常均值水平，ewma均值则迅速提升，恢复后迅速下降至正常水平
图9（β=0.9） 图10（β=0.98） 调大ewma的β值 β值越大，每次计算均值时受到之前均值影响越大，则平均曲线更加平滑，因此图10的曲线要比图9表现更加平滑，但付出的代价是对网络延迟反应也变的迟钝（但也碾压算术平均）
图9（β=0.9） 图11（β=0.32） 调小ewma的β值 β值越小，每次计算均值时受到之前均值影响越小，则平均曲线更加趋近于每次的实际耗时，因此图11的曲线要比图9表现的更加趋近于每次的实际耗时，顺理成章的，它对网络延迟的反映极迅速

通过实验，可以看出ewma的优势极大，但β的取值需要仔细斟酌，若β太小，则无法很好的体现出平均值，若β太大，很好的体现了平均值，但对网络波动的反应相对迟钝，这里就考虑到一个折中的方案：

实时调整β值，比如ewma可以在网络波动时适当降低β的值，使其快速感知到波动的存在，当网络波动结束后，适当提升β的值，这样就可以在网络稳定的情况下较好的反映一个区段内的均值情况，这样等于结合了图10和图11各自的优点，实现后将达到一种效果：快速感知网络延迟并迅速提高其均值，当网络恢复后，慢慢降回正常水平（均值恢复需要慢慢进行，因为刚恢复的节点稳定性不可信，慢慢恢复到正常水平，以信任其稳定性）

衰减函数调整β值

通过上面的要求，我们需要完善这个变化的β，那么它该如何变化呢？如何能达到碰到网络波动时迅速感知，当波动过后慢慢恢复的效果呢？慢慢恢复需要多慢？可不可以通过调整某个阈值来控制恢复的速率？

带着上面的问题，需要了解一下：衰减函数（参考：牛顿冷却定律）

计算方法为：

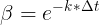
e是数学常量，△t表示第t次请求的耗时，k表示衰减系数，它的函数图如下：

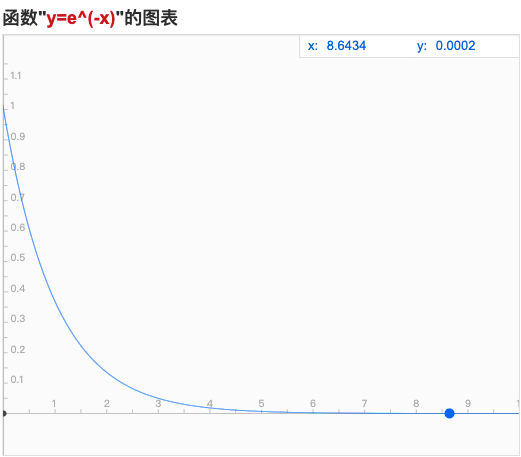
我们把k*△t看做x的取值，那么k和△t成正比，即：k和△t取值越大，β就越小

现在来看看这个结论支不支持我们要实现的功能：

  1. 网络抖动时，假设△t非常大，即便不乘k值，β值也会变得很小，这是符合我们预期的，我们需要的就是在网络抖动时，迅速感知
  2. 网络恢复时，△t迅速降低，假设此时△t非常小，则k值越大，图12里对应的x越大，β的值就越小，事实上通过实验可以得出，如果k值很大，得出的曲线近乎等于图11。 经过上面的梳理，发现k值似乎没有起到衰减作用，反而因为它的存在导致β值降低，它的取值在网络抖动恢复后依旧在削弱β的值，导致网络恢复后迅速降低到正常水平，这是我们不愿意看到的，那么上面的函数需要做下变体，即让△t和k值成反比即可：

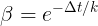
此时结论如下：

  1. 网络抖动时，假设△t非常大，即便k值起到中和作用，β值较之前也会明显变小，这是符合我们预期的，我们需要的就是在网络抖动时，迅速感知
  2. 网络恢复时，即使△t迅速降低，那么由于k值的中和（△t/k的值大小和k值成反比），k越大，β越大，则均值计算受之前波动期的均值影响越大，曲线恢复越缓慢。

这点可以通过下方的验证得到证实，调整衰减系数k，的确可以控制在遇到波动时恢复到正常水平时的速度，衰减系数设置越大，波幅越大（恢复越慢），反之越小（恢复越快）。

衰减系数验证:

第一组：随机次数的网络抖动，衰减系数分别为600和50

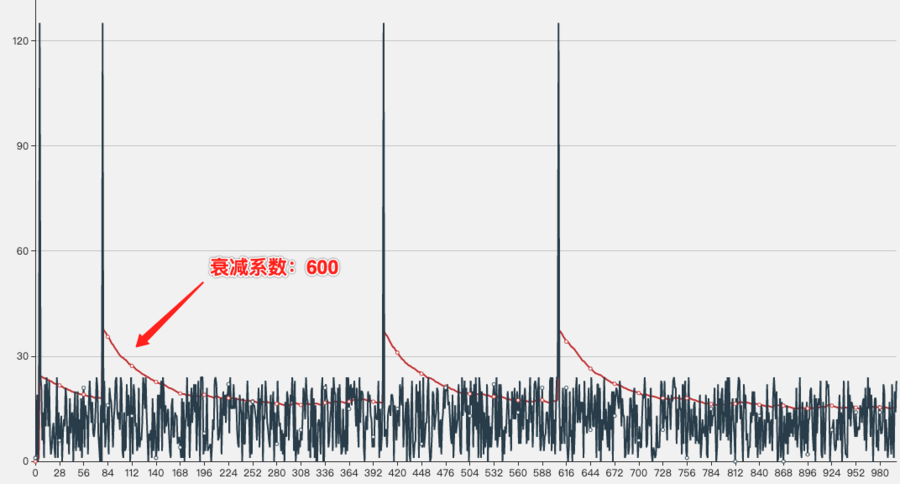
衰减系数为600时的走势图，可以看出，网络恢复后均值变化衰减速度很慢

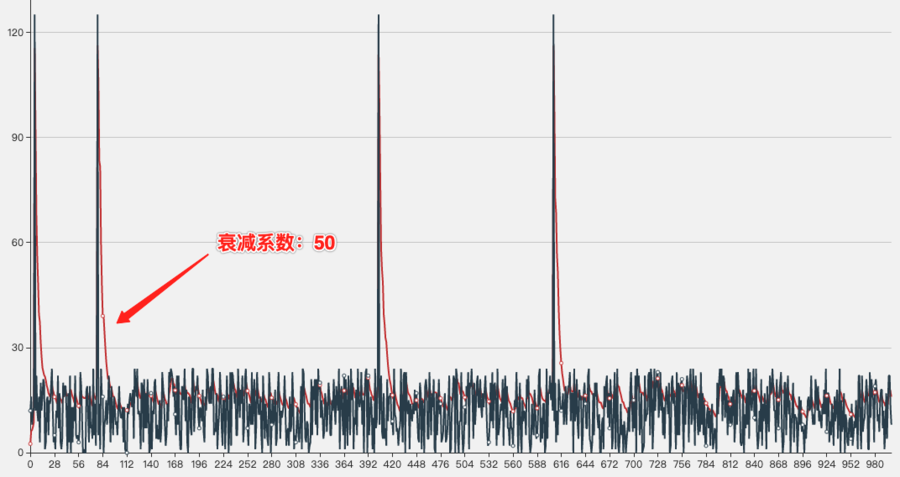
衰减系数为50时的走势图，可以看出，网络恢复后均值变化衰减速度很快

第二组：第100~200次请求响应时间扩大5倍，衰减系数仍然是600和50

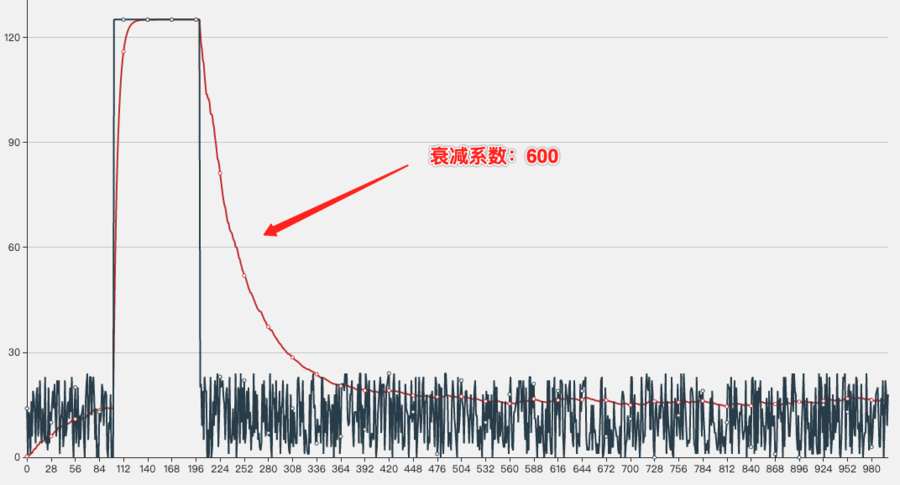
衰减系数为600时的走势图，可以看出在抖动发生时，仍然可以迅速感知，后续恢复时的衰减速度跟上面结果一样慢

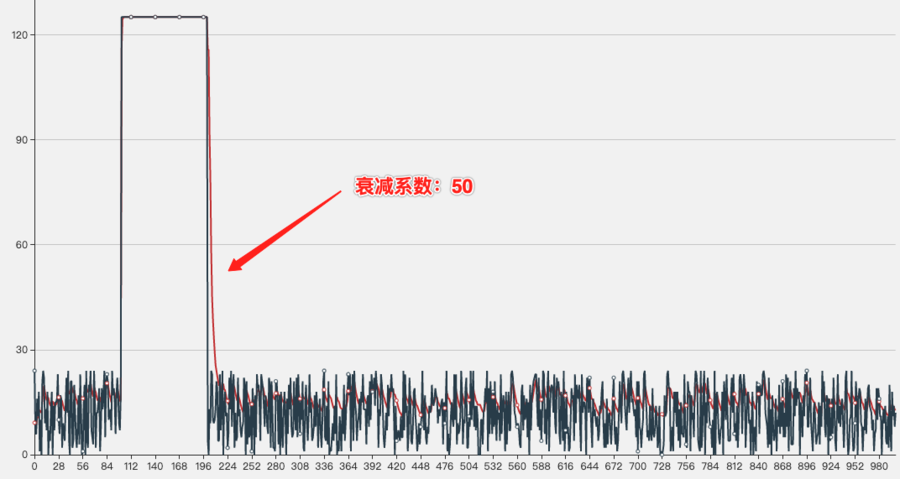
衰减系数为50时的走势图，可以看出在抖动发生时，可以非常迅速的感知，后续恢复时的衰减速度跟上面结果一样快

算法原理

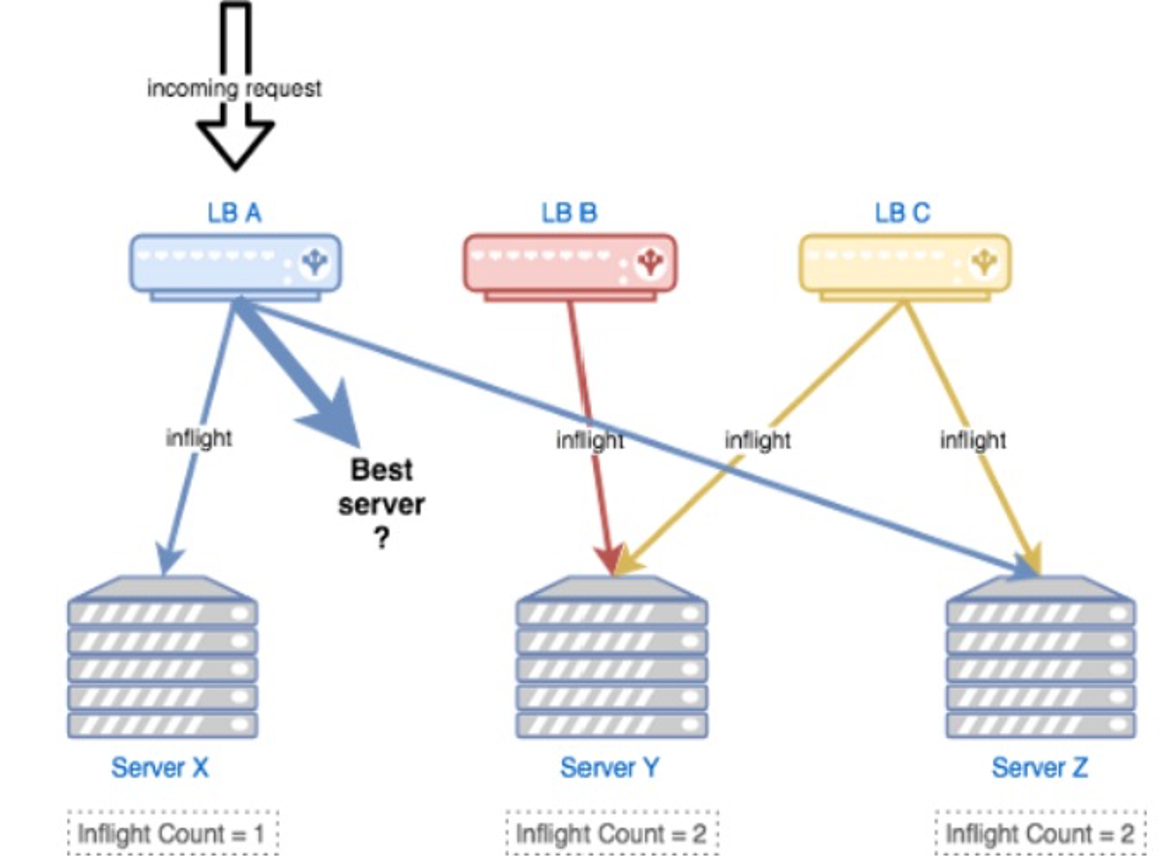
参考了《The power of two choices in randomized load balancing》的思路，我们使用 the choice-of-2 算法，随机选取的两个节点进行打分，选择更优的节点:

  • 选择 backend：CPU，client：health、inflight、latency 作为指标，使用一个简单的线性方程进行打分。
  • 对新启动的节点使用常量惩罚值(penalty)，以及使用探针方式最小化放量，进行预热。
  • 打分比较低的节点，避免进入“永久黑名单”而无法恢复，使用统计衰减的方式，让节点指标逐渐恢复到初始状态(即默认值)。 指标计算结合 moving average，使用时间衰减，计算vt = v(t-1) β + at (1-β) ，β为若干次幂的倒数即: Math.Exp((-span) / 600ms)

本算法通过随机选择两个 node 选择优胜者来避免羊群效应，并通过 ewma（指数加权移动平均法） 尽量获取服务端的实时状态。

针对 服务端 的指标： 服务端获取最近 500ms 内的 CPU 使用率（针对容器场景：需要将 cgroup 设置的限制考虑进去，并除于 CPU 核心数），并将 CPU 使用率乘与 1000 后塞入每次 gRPC 请求中的的 Trailer 中夹带返回

针对 客户端 的指标：

  • server_cpu：通过每次请求中服务端塞在 trailer 中的 cpu_usage 拿到服务端最近 500ms 内的 cpu 使用率
  • inflight：当前客户端正在发送并等待 response 的请求数（pending request）
  • latency: 加权移动平均算法计算出的接口延迟
  • client_success: 加权移动平均算法计算出的请求成功率（只记录 gRPC 内部错误，比如 context deadline）

计算权重的公式如下： (\frac{successmetaWeight}{cpu\sqrt{lag}*(inflight+1)})

这个公式的含义很直观，对权重有积极影响的因子，如成功率，初始权重等，位于分子；对权重有消极影响的因子，如cpu负载（过高）、lag延迟（过大）、以及积压的请求数inflight，放在分母的位置。（为了防止除法溢出，inflight做了加1处理）

EWMA 算法的修正（预测）公式是：

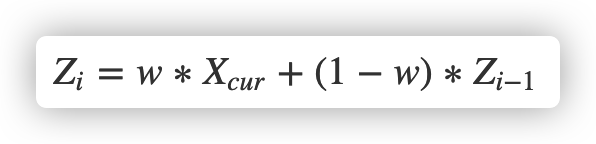
其中，在 P2C 算法中，w 系数按照下面的规则获取： w := math.Exp(float64(-td) / float64(tau))

预测的方法是，每隔一段时间进行一次采样，每次采样完成之后，就对预测值进行一次修正，这种方法的特点是近期的采样值对预测值的影响大，远期的影响较小。从算法应用场景可知，和 P2C 算法计算场景比较类似，这里针对 p2c.subConn 结构使用 EWMA 算法，只需要保存上一次计算拿到的结果即可。

代码分析

全局变量 & init

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

const (
	// The mean lifetime of `cost`, it reaches its half-life after Tau*ln(2).
	tau = int64(time.Millisecond * 600)
	// if statistic not collected,we add a big penalty to endpoint
	penalty = uint64(1000 * time.Millisecond * 250)

	forceGap = int64(time.Second * 3)
)

var _ base.PickerBuilder = &p2cPickerBuilder{}
var _ balancer.Picker = &p2cPicker{}

// Name is the name of pick of two random choices balancer.
const Name = "p2c"

// newBuilder creates a new weighted-roundrobin balancer builder.
func newBuilder() balancer.Builder {
	return base.NewBalancerBuilder(Name, &p2cPickerBuilder{}, base.Config{})
}

func init() {
	balancer.Register(newBuilder())
}

p2c.subConn

p2c.subConn，封装了 balancer.SubConn，代表了 Client 到 Server 的一条长连接，封装了核心属性（计算权重需要）： 其中重要的字段说明如下（牢记一个 subConn 代表了客户端到某个服务端 Node 的唯一属性）：

  • meta：在服务发现（Etcd）中设置的元数据值
  • lag：请求延迟（用于与下次实现加权计算）
  • success：使用加权算法拿到的客户端 RPC 调用成功率
  • inflight：当前正在处理的请求数
  • svrCPU：保存了服务端返回的最近一段时间的 CPU 使用率
  • stamp：保存上次计算权重的时间戳（Nano）
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

type subConn struct {
	// metadata
	conn balancer.SubConn
	addr resolver.Address
	meta wmd.MD

	//client statistic data
	lag      uint64
	success  uint64
	inflight int64
	// server statistic data
	svrCPU uint64

	//last collected timestamp
	stamp int64
	//last pick timestamp
	pick int64
	// request number in a period time
	reqs int64
}

p2c.subConn 实现的方法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

func (sc *subConn) valid() bool {
	return sc.health() > 500 && atomic.LoadUint64(&sc.svrCPU) < 900
}

func (sc *subConn) health() uint64 {
	return atomic.LoadUint64(&sc.success)
}

func (sc *subConn) load() uint64 {
	lag := uint64(math.Sqrt(float64(atomic.LoadUint64(&sc.lag))) + 1)
	load := atomic.LoadUint64(&sc.svrCPU) * lag * uint64(atomic.LoadInt64(&sc.inflight))
	if load == 0 {
		// penalty是初始化没有数据时的惩罚值，默认为1e9 * 250
		load = penalty
	}
	return load
}

func (sc *subConn) cost() uint64 {
	load := atomic.LoadUint64(&sc.svrCPU) * atomic.LoadUint64(&sc.lag) * uint64(atomic.LoadInt64(&sc.inflight))
	if load == 0 {
		// penalty是初始化没有数据时的惩罚值，默认为1e9 * 250
		load = penalty
	}
	return load
}

p2cPickerBuilder

p2cPickerBuilder.Build 在每次后端节点有增减的情况下调用，初始化时会调用一次，readySCs 保存了后端服务器的基础信息，从代码实现上看，也是做了对节点的初始化工作： 当后端有删减时，也会强制把已存在的后端节点进行初始化：

这里后端的初始化数据为

  • svrCPU: 500
  • lag： 0
  • success：1000
  • inflight： 1
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

type p2cPickerBuilder struct{}

func (*p2cPickerBuilder) Build(readySCs map[resolver.Address]balancer.SubConn) balancer.Picker {
	p := &p2cPicker{
		colors: make(map[string]*p2cPicker),
		// 初始化 rand 种子
		r:      rand.New(rand.NewSource(time.Now().UnixNano())),
	}

	// 初始化后端的权重数据
	for addr, sc := range readySCs {
		fmt.Println("[p2cPickerBuilder.Builder]init:",addr,sc)
		meta, ok := addr.Metadata.(wmd.MD)
		if !ok {
			meta = wmd.MD{
				Weight: 10,
			}
		}
		subc := &subConn{
			conn: sc,
			addr: addr,
			meta: meta,

			svrCPU:   500,
			lag:      0,
			success:  1000,
			inflight: 1,
		}
		if meta.Color == "" {
			p.subConns = append(p.subConns, subc)
			continue
		}
		// if color not empty, use color picker
		// 如果服务端定义了 color 筛选，则启动 color 的选择逻辑（测试时没用）
		cp, ok := p.colors[meta.Color]
		if !ok {
			cp = &p2cPicker{r: rand.New(rand.NewSource(time.Now().UnixNano()))}
			p.colors[meta.Color] = cp
		}
		cp.subConns = append(cp.subConns, subc)
	}
	return p
}

p2cPicker

p2c.Picker 实现了负载均衡的选择逻辑：

  1. Pick：主方法入口
  2. 先调用 prePick，选择两个随机的 node
  3. 最后从上一步的 node 列表中选取一个合适的 node，返回其对应的subConn，执行 RPC 请求
  4. 根据RPC请求结果及 node 回带的服务端 CPU 字段信息，更新本 subConn 的核心因子信息
    • stamp
    • success
    • lag

p2cPicker 结构：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

type p2cPicker struct {
	// subConns is the snapshot of the weighted-roundrobin balancer when this picker was
	// created. The slice is immutable. Each Get() will do a round robin
	// selection from it and return the selected SubConn.
	subConns []*subConn		// 保存所有的后端
	colors   map[string]*p2cPicker
	logTs    int64		//
	r        *rand.Rand
	lk       sync.Mutex
}

接下来着重分析下 pick 和 prePick 方法：

prePick 方法，实现了随机选择的逻辑，总循环 3 次，随机从 subConns []*subConn 中选择两个节点 nodeB 和 nodeA，如果满足 node.valid() 的要求，直接返回，不满足的话，返回最后一次的选择的两个节点： 注意返回值中的 nodeA 和 nodeB 都是 subConn 结构。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// choose two distinct nodes
func (p *p2cPicker) prePick() (nodeA *subConn, nodeB *subConn) {
	for i := 0; i < 3; i++ {
		p.lk.Lock()
		a := p.r.Intn(len(p.subConns))
		b := p.r.Intn(len(p.subConns) - 1)
		p.lk.Unlock()
		if b >= a {
			b = b + 1
		}
		nodeA, nodeB = p.subConns[a], p.subConns[b]
		if nodeA.valid() || nodeB.valid() {
			break
		}
	}
	return
}

picker 的实现如下，重要部分已加了注释，需要关注的有如下几点信息：

  1. DoneInfo() 是在 RPC 方法执行完成后的回调，主要用于在 gRPC 的 Trailer 返回的 pc 对应的服务端 CPU 信息，根据此 CPU 信息，更新 pc 这个 subConn 的相关信息
  2. 计算权重分数的方法，每次请求来时我们都会更新延迟，并且把之前获得的时间延迟进行权重的衰减，新获得的时间提高权重，这样就实现了滚动更新
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

func (p *p2cPicker) Pick(opts balancer.PickInfo) (balancer.PickResult, error) {
	// FIXME refactor to unify the color logic
	color := nmd.String(opts.Ctx, nmd.Color)
	if color == "" && env.Color != "" {
		color = env.Color
	}
	if color != "" {
		if cp, ok := p.colors[color]; ok {
			return cp.pick(opts)
		}
	}
	return p.pick(opts)
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96

func (p *p2cPicker) pick(opts balancer.PickInfo) (balancer.PickResult, error) {
	var pc, upc *subConn
	start := time.Now().UnixNano()

	if len(p.subConns) <= 0 {
		return balancer.PickResult{}, balancer.ErrNoSubConnAvailable
	} else if len(p.subConns) == 1 {
        // 只有 1 个节点，直接返回
		pc = p.subConns[0]
	} else {
		nodeA, nodeB := p.prePick()
		// meta.Weight为服务发布者在disocvery中设置的权重
		if nodeA.load()*nodeB.health()*nodeB.meta.Weight > nodeB.load()*nodeA.health()*nodeA.meta.Weight {
            //pc 为本次算法选择的节点
			pc, upc = nodeB, nodeA
		} else {
			pc, upc = nodeA, nodeB
		}
		// 如果选中的节点，在forceGap期间内没有被选中一次，那么强制一次
		// 利用强制的机会，来触发成功率、延迟的衰减
		// 原子锁conn.pick保证并发安全，放行一次
		pick := atomic.LoadInt64(&upc.pick)
		if start-pick > forceGap && atomic.CompareAndSwapInt64(&upc.pick, pick, start) {
			pc = upc
		}
	}

	// 节点未发生切换才更新pick时间
	if pc != upc {
		atomic.StoreInt64(&pc.pick, start)
	}
	atomic.AddInt64(&pc.inflight, 1)
	atomic.AddInt64(&pc.reqs, 1)
    // RPC 方法执行完成后，更新状态
	return balancer.PickResult{
		SubConn: pc.conn,
		Done: func(di balancer.DoneInfo) {
            // 当前正在处理的请求数减 1，好理解
			atomic.AddInt64(&pc.inflight, -1)
            // 取当前的时间戳（Nano）
			now := time.Now().UnixNano()
			// get moving average ratio w
            // 获取 && 设置上次测算的时间点，将 pc.stamp 的值更新为 now
			stamp := atomic.SwapInt64(&pc.stamp, now)
            // 获取时间间隔
			td := now - stamp
			if td < 0 {
				td = 0
			}
            // 获取时间衰减系数
			w := math.Exp(float64(-td) / float64(tau))
            // 获得本次延迟数据 1（注意 start 是在 pick 开始计时的）
			lag := now - start
			if lag < 0 {
				lag = 0
			}
            // 获取上次保存的延迟数据 2
			oldLag := atomic.LoadUint64(&pc.lag)
			if oldLag == 0 {
				w = 0.0
			}
            // 延迟数据 1 与延迟数据 2，计算出平均延迟（EWMA）
			lag = int64(float64(oldLag)*w + float64(lag)*(1.0-w))
            // 保存本地计算出的延迟数据
			atomic.StoreUint64(&pc.lag, uint64(lag))

			success := uint64(1000) // error value ,if error set 1
			if di.Err != nil {
				if st, ok := status.FromError(di.Err); ok {
					// only counter the local grpc error, ignore any business error
					if st.Code() != codes.Unknown && st.Code() != codes.OK {
						success = 0
					}
				}
			}
			oldSuc := atomic.LoadUint64(&pc.success)
			success = uint64(float64(oldSuc)*w + float64(success)*(1.0-w))
			atomic.StoreUint64(&pc.success, success)
            // 从服务端的 Trailer 中拿到 CPU 的值
			trailer := di.Trailer
			if strs, ok := trailer[wmd.CPUUsage]; ok {
				if cpu, err2 := strconv.ParseUint(strs[0], 10, 64); err2 == nil && cpu > 0 {
					atomic.StoreUint64(&pc.svrCPU, cpu)
				}
			}

			logTs := atomic.LoadInt64(&p.logTs)
			if now-logTs > int64(time.Second*3) {
                // 超过一个 3s 的周期，尝试打印当前状态
				if atomic.CompareAndSwapInt64(&p.logTs, logTs, now) {
					p.printStats()
				}
			}
		},
	}, nil
}

trailer需要另一个服务端在返回请求时传入,通常加在中间件里面:

1
2
3
4
5
6
7
8
9

func stats() grpc.UnaryServerInterceptor {
        return func(ctx context.Context, req interface{}, args *grpc.UnaryServerInfo, handler grpc.UnaryHandler) (resp interface{}, err error) {
                resp, err = handler(ctx, req)
                trailer := metadata.Pairs([]string{"serverinfo", "enjoy"}...)
                // 每次 rpc 请求时，放在 tailer，上报至 discovery
                grpc.SetTrailer(ctx, trailer)
                return
        }
}

参考

The Power of Two Random Choices

深入解析TensorFlow中滑动平均模型与代码实现

负载均衡-P2C算法

Kratos 源码分析：分析 Warden 框架 Dynamic-WRR 负载均衡算法的实现

Kratos 源码分析：Warden 负载均衡算法之 P2C