算法目标

kmp算法完成的任务是：给定两个字符串O和f，长度分别为n和m，判断f是否在O中出现，如果出现则返回出现的位置。常规方法是遍历a的每一个位置，然后从该位置开始和b进行匹配，但是这种方法的复杂度是O(nm)。kmp算法通过一个O(m)的预处理，使匹配的复杂度降为O(n+m)。

算法思想

next数组计算

next 数组的求解基于 “前缀” 和“后缀”，即next[i]等于P[0]…P[i - 1]最长的相同前后缀的长度（请暂时忽视 i 等于 0 时的情况，下面会有解释）。我们依旧以上述的表格为例，为了方便阅读，我复制在下方了。

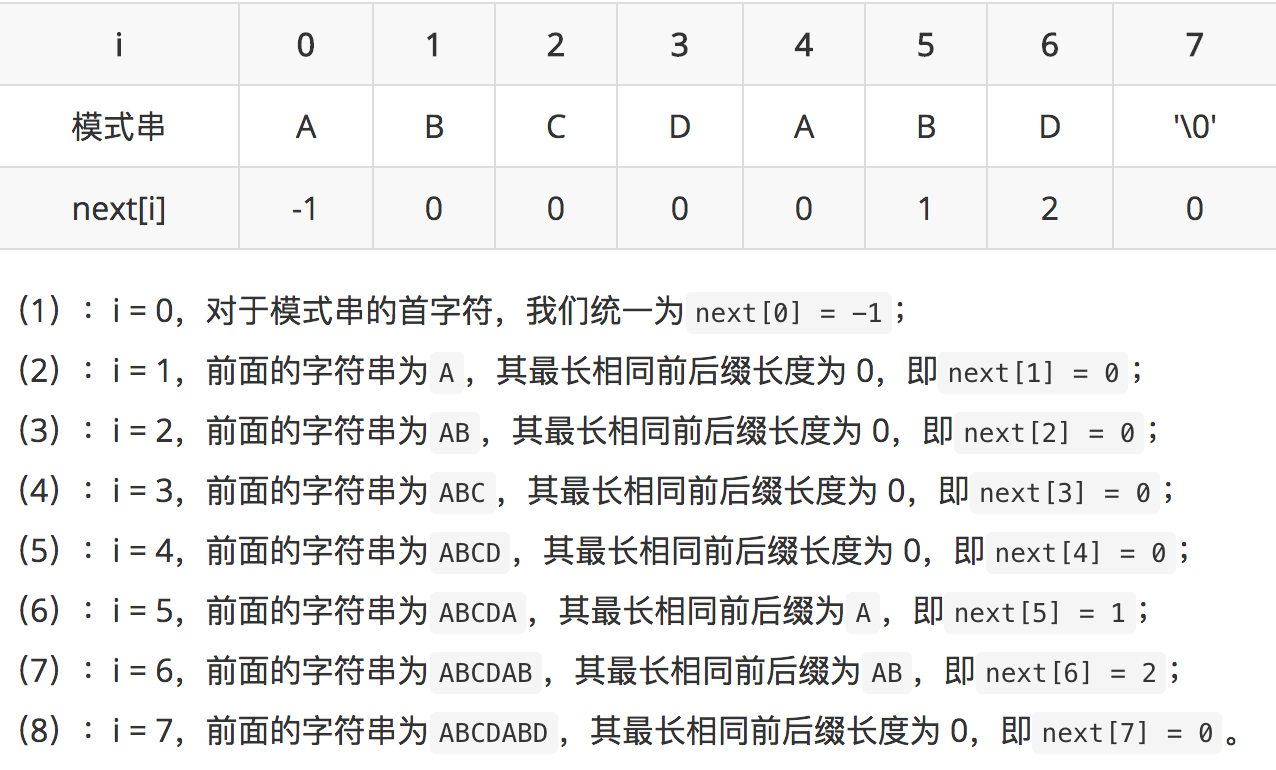
那么，为什么根据最长相同前后缀的长度就可以实现在不匹配情况下的跳转呢？举个代表性的例子：假如i = 6时不匹配，此时我们是知道其位置前的字符串为ABCDAB，仔细观察这个字符串，首尾都有一个AB，既然在i = 6处的 D 不匹配，我们为何不直接把i = 2处的 C 拿过来继续比较呢，因为都有一个AB啊，而这个AB就是ABCDAB的最长相同前后缀，其长度 2 正好是跳转的下标位置。

若在i = 5时匹配失败，此时应该把i = 1处的字符拿过来继续比较，但是这两个位置的字符是一样的，都是B，既然一样，拿过来比较不就是无用功了么？之所以会这样是因为 KMP 不够完美。那怎么改写代码就可以解决这个问题呢？很简单。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

void getNext(int *next, string &needle,int lenb) {
    int i = 0, j = -1;
    next[0] = -1;
    while (i < lenb - 1) {
        while (j != -1 && needle[i] != needle[j]) j = next[j];//next数组表示每个元素的失配位置
        ++i; ++j;
        //特殊情况，这里即为优化之处。考虑下AAAAB, 防止4个A形成0123在匹配时多次迭代。
        //之前可以得到i-1和j-1的拥有公共的前缀后缀。当前是i发生失配，如果i和j相等，那么j怎么可能合适？所以直接找j的失配位即可
        if (needle[i] == needle[j]) next[i] = next[j];
        else next[i] = j;
    }
}

细心的朋友会问 while语句中j != -1存在的意义是何？第一，程序刚运行时，j 是被初始为 - 1，直接进行P[i] == P[j]判断无疑会边界溢出；第二，else 语句中j = next[j]，j 是不断后退的，若 j 在后退中被赋值为 - 1（也就是j = next[0]），在P[i] == P[j]判断也会边界溢出。综上两点，其意义就是为了特殊边界判断。

字符串匹配

计算完成next数组之后，我们就可以利用next数组在字符串O中寻找字符串f的出现位置。匹配的代码和求next数组的代码非常相似，因为匹配的过程和求next数组的过程其实是一样的。假设现在字符串f的前i个位置都和从某个位置开始的字符串O匹配，现在比较第i+1个位置。如果第i+1个位置相同，接着比较第i+2个位置；如果第i+1个位置不同，则出现不匹配，我们依旧要将长度为i的字符串分割，获得其最大公共长度next[i]，然后从next[i]继续比较两个字符串。这个过程和求next数组一致，所以可以匹配代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int findAppearance(string haystack, int lena, string needle,int lenb) {
    if (haystack.empty()) return needle.empty() ? 0 : -1;
    if (needle.empty()) return 0;
    int next[lenb + 1];//长度要比字符串大1
    getNext(next, needle,lenb);//求得needle的next值
    int i = 0, j = 0;
    while (i != lena) {//kmp匹配（i代表模板串，j代表匹配串）
        while (j != -1 && haystack[i] != needle[j]) j = next[j];
        ++i; ++j;
        if (j == lenb) return i - j;//i是当前母串的位置，j现在是匹配串的长度
    }
    return -1;
}

复杂度

kmp算法的复杂度是O(n+m)，可以采用均摊分析来解答，具体可参考算法导论。