函数式编程
函数式编程是很多语言正在支持或已经支持的日渐流行的编程范式。Go 已经支持了其中一部分的特性,比如头等函数和更高阶功能的支持,使函数式编程成为可能。
什么是函数式编程?
函数式编程,是指忽略(通常是不允许)可变数据(以避免它处可改变的数据引发的边际效应),忽略程序执行状态(不允许隐式的、隐藏的、不可见的状态),通过函数作为入参,函数作为返回值的方式进行计算,通过不断的推进(迭代、递归)这种计算,从而从输入得到输出的编程范式。在函数式编程范式中,没有过程式编程所常见的概念:语句,过程控制(条件,循环等等)。此外,在函数式编程范式中,具有引用透明(Referential Transparency)的特性,此概念的含义是函数的运行仅仅和入参有关,入参相同则出参必然总是相同,函数本身(被视作f(x))所完成的变换是确定的。
顺便一提,柯里化 是函数式编程中相当重要的一个理论和技术。完全抛弃过程式编程的 if、then、while 之类的东西,完全的函数迭代,一般是纯函数式支持者最为喜爱的,而诸如 Start(…).Then(…).Then(…).Else(…).Finally(…).Stop() 这类风格往往会被视为异教徒。
总结一下,函数式编程具有以下的表征:
- No Data mutations 没有数据易变性
- No implicit state 没有隐式状态
- No side effects 没有边际效应(没有副作用)
- Pure functions only 只有纯粹的函数,没有过程控制或者语句
- First-class function 头等函数身份
- First-class citizen 函数具有一等公民身份
- Higher-order functions 高阶函数,可以出现在任何地方
- Closures 闭包 - 具有上级环境捕俘能力的函数实例
- Currying 柯里化演算2 - 规约多个入参到单个,等等
- Recursion 递归运算 - 函数嵌套迭代以求值,没有过程控制的概念
- Lazy evaluations / Evaluation strategy 惰性求值 - 延迟被捕俘变量的求值到使用时
- Referential transparency 引用透明性 - 对于相同的输入,表达式的值必须相同,并且其评估必须没有副作用
函数式编程的优势是什么?
函数式编程是让开发者提升代码质量的一些模式。这些质量提升的模式并非函数式编程独有,而是一些 “免费” 的优势。
- 可测性 - 测试纯函数更加简单,因为函数永远不会产生超出作用范围的影响(比如,终端输出、数据库的读取),并总会得到可预测的结果
- 可表达性 - 函数式编程/库使用声明式的基础可以更高效地表达函数的原始意图,尽管需要额外学习这些基础
- 可理解性 - 阅读和理解没有副作用、全局或可变的纯函数主观来看更简单
正如多数开发者从经验中学到的,如 Robert C. Martin 在代码整洁之道中所说:
1
|
确实,相对于写代码,花费在读代码上的时间超过 10 倍。为了写出新代码,我们一直在读旧代码。…[因此,] 让代码更易读,可以让代码更易写。
|
根据团队的经验或学习函数式编程的意愿,这些优势会产生很大的影响。相反,对于缺乏经验和足够时间投入学习的团队,或维护大型的代码仓库时,函数式编程将会产生相反的作用,上下文切换的引入或显著的重构工作将无法产生相应的价值。
Go 函数式编程
什么是“一等公民”
关于什么是编程语言的“一等公民”,业界并没有教科书给出精准的定义。这里引用一下 wiki 发明人、C2 站点作者沃德·坎宁安(Ward Cunningham)对“一等公民”的诠释:
如果一门编程语言对某种语言元素的创建和使用没有限制,我们可以像对待值(value)一样对待这种语法元素,那么我们就称这种语法元素是这门编程语言的“一等公民”。拥有“一等公民”待遇的语法元素可以存储在变量中,可以作为函数传递给函数,可以在函数内部创建并可以作为返回值从函数返回。在动态类型语言中,语言运行时还支持对“一等公民”类型的检查。
基于上面关于“一等公民”的诠释,我们来看看 Go 语言的函数是如何满足上述条件而成为“一等公民”的。
正常创建
我们可以在源码顶层正常创建一个函数,如下面的函数 newPrinter:
1
2
3
4
5
6
7
8
9
|
// $GOROOT/src/fmt/print.go
func newPrinter() *pp {
p := ppFree.Get().(*pp)
p.panicking = false
p.erroring = false
p.wrapErrs = false
p.fmt.init(&p.buf)
return p
}
|
在函数内创建
在 Go 语言中,我们可以在函数内定义一个新函数,如下面代码中在 hexdumpWords 函数内部定义的匿名函数(被赋值给变量 p1)。在 C/C++中我们无法实现这一点,这也是 C/C++语言中函数不是“一等公民”的原因之一。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// $GOROOT/src/runtime/print.go
func hexdumpWords(p, end uintptr, mark func(uintptr) byte) {
p1 := func(x uintptr) {
var buf [2 * sys.PtrSize]byte
for i := len(buf) - 1; i >= 0; i-- {
if x&0xF < 10 {
buf[i] = byte(x&0xF) + '0'
} else {
buf[i] = byte(x&0xF) - 10 + 'a'
}
x >>= 4
}
gwrite(buf[:])
}
... ...
}
|
作为类型
我们可以使用函数来自定义类型,如下面代码中的 HandlerFunc、visitFunc 和 action:
1
2
3
4
5
6
7
8
|
// $GOROOT/src/net/http/server.go
type HandlerFunc func(ResponseWriter, *Request)
// $GOROOT/src/sort/genzfunc.go
type visitFunc func(ast.Node) ast.Visitor
// codewalk: <https://tip.golang.org/doc/codewalk/functions/>
type action func(current score) (result score, turnIsOver bool)
|
存储到变量中
我们可以将定义好的函数存储到一个变量中,如下面代码中的 apply:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// $GOROOT/src/runtime/vdso_linux.go
func vdsoParseSymbols(info *vdsoInfo, version int32) {
if !info.valid {
return
}
apply := func(symIndex uint32, k vdsoSymbolKey) bool {
sym := &info.symtab[symIndex]
typ := _ELF_ST_TYPE(sym.st_info)
bind := _ELF_ST_BIND(sym.st_info)
... ...
*k.ptr = info.loadOffset + uintptr(sym.st_value)
return true
}
... ...
}
|
作为参数传入函数
我们可以将函数作为参数传入函数,比如下面代码中函数 AfterFunc 的参数 f:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
$GOROOT/src/time/sleep.go
func AfterFunc(d Duration, f func()) *Timer {
t := &Timer{
r: runtimeTimer{
when: when(d),
f: goFunc,
arg: f,
},
}
startTimer(&t.r)
return t
}
|
作为返回值从函数返回
函数还可以被作为返回值从函数返回,如下面代码中函数 makeCutsetFunc 的返回值就是一个函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// $GOROOT/src/strings/strings.go
func makeCutsetFunc(cutset string) func(rune) bool {
if len(cutset) == 1 && cutset[0] < utf8.RuneSelf {
return func(r rune) bool {
return r == rune(cutset[0])
}
}
if as, isASCII := makeASCIISet(cutset); isASCII {
return func(r rune) bool {
return r < utf8.RuneSelf && as.contains(byte(r))
}
}
return func(r rune) bool { return IndexRune(cutset, r) >= 0 }
}
|
我们看到:就像沃德·坎宁安(Ward Cunningham)对“一等公民”的诠释中所说的那样,Go 中的函数可以像普通整型值那样被创建和使用。
除了上面那些例子,函数还可以被放入数组/切片/map 等结构中、可以像其他类型变量一样被赋值给 interface{}、甚至我们可以建立元素为函数的 channel,如下面例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// function_as_first_class_citizen_1.go
package main
import "fmt"
type binaryCalcFunc func(int, int) int
func main() {
var i interface{} = binaryCalcFunc(func(x, y int) int { return x + y })
c := make(chan func(int, int) int, 10)
fns := []binaryCalcFunc{
func(x, y int) int { return x + y },
func(x, y int) int { return x - y },
func(x, y int) int { return x * y },
func(x, y int) int { return x / y },
func(x, y int) int { return x % y },
}
c <- func(x, y int) int {
return x * y
}
fmt.Println(fns[0](5, 6))
f := <-c
fmt.Println(f(7, 10))
v, ok := i.(binaryCalcFunc)
if !ok {
fmt.Println("type assertion error")
return
}
fmt.Println(v(17, 7))
}
|
和 C/C++这类语言相比,作为“一等公民”的 Go 函数拥有难得的"灵活性"。
语言特性
函数式编程的语言支持包括一系列从仅支持函数范式(比如 Haskell)到多范式和头等函数的支持(比如 Scale、Elixir),还包括多范式和部分支持(如 Javascript、Go)。在后面的语言中,函数式编程的支持一般是通过使用社区创建的库,它们复制了前面两个语言的部分或全部的标准库的特性。
属于后一种类别的 Go 要使用函数式编程需要下面这些特性:
| 语言特性 |
支持情况 |
| 头等函数和高阶函数 |
✓ |
| 闭包 |
✓ |
| 泛型 |
✓† |
| 尾部调用优化 |
✗ |
| 可变参数函数 + 可变类型参数 |
✗ |
| 柯里化 |
✗ |
† 将在 Go 1.18 中可用(2022 年初)
现有的库
在 Go 生态中,有大量函数式编程的库,区别在于流行度、特性和工效。由于缺少泛型,它们全部只能从下面两种选择中取一个:
- 类型安全和特定使用场景 - 选择这个方法的库实现的设计是类型安全,但只能处理特定的预定义类型。因为无法应用于自适应的类型或结构体,这些库的应用范围将受限制。
- 比如,
func UniqString(data []string) []string 和 func UniqInt(data []int) []int 都是类型安全的,但只能应用在预定义的类型
- 类型不安全和未知的应用场景 - 选择这个方法的库实现的是类型不安全但可以应用在任意使用场景的方法。这些库可以处理自定义类型和结构体,但折衷点在于必须使用类型断言,这让应用在不合理的实现时有运行时崩溃的风险。
- 比如,一个通用的函数可能有这样的命名:
func Uniq(data interface{}) interface{}
这两种设计选择显示了两种相似的不吸引人的选项:有限的使用或运行时崩溃的风险。最简单也许最常见的选择是不使用 Go 的函数式编程库,坚持指令式的风格。
函数的显示转型
Go 是类型安全的语言,Go 语言不允许隐式类型转换,因此下面的代码是无法通过编译的:
1
2
3
|
var a int = 5
var b int32 = 6
fmt.Println(a + b) // 违法操作: a + b (不匹配的类型int和int32)
|
我们必须通过对上面代码进行显式的转型才能通过编译器的检查:
1
2
3
|
var a int = 5
var b int32 = 6
fmt.Println(a + int(b)) // ok。输出11
|
函数是“一等公民”,对整型变量进行的操作也同样可以用在函数上面,即函数也可以被显式转型,并且这样的转型在特定的领域具有奇妙的作用。一个最为典型的示例就是 http.HandlerFunc 这个类型,我们来看一下例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
// function_as_first_class_citizen_2.go
package main
import (
"fmt"
"net/http"
)
func greeting(w http.ResponseWriter, r *http.Request) {
fmt.Fprintf(w, "Welcome, Gopher!\n")
}
func main() {
http.ListenAndServe(":8080", http.HandlerFunc(greeting))
}
|
上述代码是我们日常最为常见的一个用 Go 构建的 Web Server 的例子。其工作机制很简单,当用户通过浏览器或类似 curl 这样的命令行工具访问 Web server 的 8080 端口时,会收到“Welcome, Gopher!”一行文字版应答。很多 Gopher 可能并未真正深入分析过这段代码,这里用到的恰恰是函数作为“一等公民”的特性,我们来看一下。
我们先来看一下 ListenAndServe 的源码:
1
2
3
4
5
|
// $GOROOT/src/net/http/server.go
func ListenAndServe(addr string, handler Handler) error {
server := &Server{Addr: addr, Handler: handler}
return server.ListenAndServe()
}
|
ListenAndServe 会将来自客户端的 http 请求交给其第二个参数 handler 处理,而这里 handler 参数的类型 http.Handler 接口:
1
2
3
4
|
// $GOROOT/src/net/http/server.go
type Handler interface {
ServeHTTP(ResponseWriter, *Request)
}
|
该接口仅有一个方法:ServeHTTP,其原型为:func(http.ResponseWriter, *http.Request)。这与我们自己定义的 http 请求处理函数 greeting 的原型是一致的。但是我们没法直接将 greeting 作为参数值传入,否则会报下面错误:
1
|
func(http.ResponseWriter, *http.Request) does not implement http.Handler (missing ServeHTTP method)
|
即函数 greeting 并未实现接口 Handler 的方法,无法将其赋值给 Handler 类型的参数。
在代码中我们也并未直接将 greeting 传入 ListenAndServe,而是将 http.HandlerFunc(greeting)作为参数传给了 ListenAndServe。我们来看看 http.HandlerFunc 是什么?
1
2
3
4
5
6
7
8
|
// $GOROOT/src/net/http/server.go
type HandlerFunc func(ResponseWriter, *Request)
// ServeHTTP calls f(w, r).
func (f HandlerFunc) ServeHTTP(w ResponseWriter, r *Request) {
f(w, r)
}
|
HandlerFunc 其实就是一个基于函数定义的新类型,它的底层类型为 func(ResponseWriter, *Request)。该类型有一个方法 ServeHTTP,继而实现了 Handler 接口。也就是说 http.HandlerFunc(greeting)这句代码的真正含义是将函数 greeting 显式转换为 HandlerFunc 类型,后者实现了 Handler 接口,满足 ListenAndServe 函数第二个参数的要求。
另外,之所以 http.HandlerFunc(greeting)这个语句可以通过编译器检查,正是因为 HandlerFunc 的底层类型正是 func(ResponseWriter, *Request),与 greeting 的原型是一致的。这和下面整型变量的转型原理并无二致:
1
2
3
|
type MyInt int
var x int = 5
y := MyInt(x) // MyInt的底层类型为int,类比 HandlerFunc的底层类型为func(ResponseWriter, *Request)
|
为了充分理解这种显式转型的“技巧”,我们再来看一个简化后的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// function_as_first_class_citizen_3.go
package main
import "fmt"
type BinaryAdder interface {
Add(int, int) int
}
type MyAdderFunc func(int, int) int
func (f MyAdderFunc) Add(x, y int) int {
return f(x, y)
}
func MyAdd(x, y int) int {
return x + y
}
func main() {
var i BinaryAdder = MyAdderFunc(MyAdd)
fmt.Println(i.Add(5, 6))
}
|
和 Web server 那个例子一样,我们想将 MyAdd 这个函数赋值给 BinaryAdder 这个接口,直接赋值是不行的,我们需要一个底层函数类型与 MyAdd 一致的自定义类型的显式转换,这个自定义类型就是 MyAdderFunc,该类型实现了 BinaryAdder 接口,这样在经过 MyAdderFunc 的显式转型后,MyAdd 被赋值给了 BinaryAdder 的变量 i。这样通过 i 调用的 Add 方法实质上就是我们的 MyAdd 函数。
高阶函数与装饰器模式
高阶函数,就是接收其他函数作为参数传入,或者把其他函数作为结果返回的函数。
高阶函数是函数式编程的重要特性,我们可以通过它实现很多高级功能,我们以一个乘法运算函数为例,来演示如何在 Go 语言中通过高阶函数来实现装饰器模式。
先编写这个乘法运算函数和调用代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
package main
import "fmt"
func multiply(a, b int) int {
return a * b
}
func main() {
a := 2
b := 8
c := multiply(a, b)
fmt.Printf("%d x %d = %d\n", a, b, c)
}
|
运行上述代码,打印结果如下:
现在,我们想要在不修改现有 multiply 函数代码的前提下计算乘法运算的执行时间,显然,这可以引入装饰器模式来实现。需要借助高阶函数来实现这个计算耗时的装饰器,对应实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
package main
import (
"fmt"
"time"
)
// 为函数类型设置别名提高代码可读性
type MultiPlyFunc func(int, int) int
// 乘法运算函数
func multiply(a, b int) int {
return a * b
}
// 通过高阶函数在不侵入原有函数实现的前提下计算乘法函数执行时间
func execTime(f MultiPlyFunc) MultiPlyFunc {
return func(a, b int) int {
start := time.Now() // 起始时间
c := f(a, b) // 执行乘法运算函数
end := time.Since(start) // 函数执行完毕耗时
fmt.Printf("--- 执行耗时: %v ---\n", end)
return c // 返回计算结果
}
}
func main() {
a := 2
b := 8
// 通过修饰器调用乘法函数,返回的是一个匿名函数
decorator := execTime(multiply)
// 执行修饰器返回函数
c := decorator(a, b)
fmt.Printf("%d x %d = %d\n", a, b, c)
}
|
我们来分析下这段代码,首先,我们通过 type 语句为匿名函数类型设置了别名 MultiPlyFunc,这样一来,后续就可以用这个类型别名来声明对应的函数类型参数和返回值,提高代码可读性。
然后是装饰器模式实现代码 execTime 函数,这是一个以 MultiPlyFunc 类型为参数和返回值的函数,所以是个高阶函数,我们看下具体实现代码:
- 在返回的 MultiPlyFunc 类型匿名函数体中,真正执行乘法运算函数 f 前,先通过 time.Now() 获取当前系统时间,并将其赋值给 start 变量;
- 然后执行 f 函数,将返回值赋值给变量 c;
- 接下来,通过 time.Since(start) 计算从 start 到现在经过的时间,也就是 f 函数执行耗时,将结果赋值给 end 变量并打印出来;
- 最后返回 f 函数运行结果 c 作为最终返回值。
核心思路就是在被修饰的功能模块(这里是外部传入的乘法函数 f)执行前后加上一些额外的业务逻辑,而又不影响原有功能模块的执行。显然,装饰器模式是遵循 SOLID 设计原则中的开放封闭原则的 —— 对代码扩展开放,对代码修改关闭。
在 main 函数中调用乘法函数 multiply 时,如果要应用装饰器,需要通过装饰器 execTime 包裹,装饰器返回的是个匿名函数,所以需要再度调用才能真正执行,执行后的打印结果如下:
1
2
|
--- 执行耗时: 83ns ---
2 x 8 = 16
|
可以看到,这次因为应用了装饰器,所以打印出了执行耗时。
为了更好地体现装饰器模式的优势,我们还可以在此基础上实现一个比较位运算和算术运算性能的程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
package main
import (
"fmt"
"time"
)
// 为函数类型设置别名提高代码可读性
type MultiPlyFunc func(int, int) int
// 乘法运算函数1(算术运算)
func multiply1(a, b int) int {
return a * b
}
// 乘法运算函数2(位运算)
func multiply2(a, b int) int {
return a << b
}
// 通过高阶函数在不侵入原有函数实现的前提下计算乘法函数执行时间
func execTime(f MultiPlyFunc) MultiPlyFunc {
return func(a, b int) int {
start := time.Now() // 起始时间
c := f(a, b) // 执行乘法运算函数
end := time.Since(start) // 函数执行完毕耗时
fmt.Printf("--- 执行耗时: %v ---\n", end)
return c // 返回计算结果
}
}
func main() {
a := 2
b := 8
fmt.Println("算术运算:")
decorator1 := execTime(multiply1)
c := decorator1(a, b)
fmt.Printf("%d x %d = %d\n", a, b, c)
fmt.Println("位运算:")
decorator2 := execTime(multiply2)
a = 1
b = 4
c = decorator2(a, b)
fmt.Printf("%d << %d = %d\n", a, b, c)
}
|
原有的代码逻辑不需要做任何变动,只需要新增一个位运算版乘法实现函数 multiply2,然后套上装饰器函数 execTime 计算耗时,最后与算术运算版乘法实现函数 multiply1 耗时做下对比即可.
通过装饰器模式,只需要为基础修饰功能编写一次代码,后面新的业务逻辑只需要维护新增部分即可,不需要侵入原有功能模块,让代码的可维护性和可读性更好。
闭包
在函数、高阶函数身属一阶公民的编程语言中,你当然可以将函数赋值为一个变量、复制给一个成员,作为另一函数的参数(或之一)进行传参,作为另一函数的返回值(或之一)。
Golang 具备上述支持。
然而,Golang 没有匿名函数外扩或缩减的语法糖,实际上,Golang 没有大多数的语法糖,这是它的设计哲学所决定的。所以你必须采用有点冗长的代码书写,而无法让语法显得简洁。
在 Golang 中,你需要完整地编写高阶函数的原型,哪怕你对其作了 type 定义也没用:
1
2
3
4
5
6
7
8
9
10
11
|
type Handler func (a int)
func xc(pa int, handler Handler) {
handler(pa)
}
func Test1(){
xc(1, func(a int){ // <- 老老实实地再写一遍原型吧
print (a)
})
}
|
值得注意的是,一旦 Handler 的原型发生变化,库作者和库使用者都会很痛苦地到处查找和修改。
对的,你将在这里学到一个编程的重要原则,接口设计必须考虑稳固性。只要接口稳固,当然不会有 Handler 的原型需要调整的可能性,对不对?
柯里化定义
我们来看一种函数式编程的典型应用:柯里化函数(currying)。在计算机科学中,柯里化是把接受多个参数的函数变换成接受一个单一参数(原函数的第一个参数)的函数,并且返回接受余下的参数和返回结果的新函数的技术。这个技术以逻辑学家 Haskell Curry 命名。
定义总是拗口难懂,我们来用 Go 编写一个直观的柯里化函数的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// function_as_first_class_citizen_4.go
package main
import "fmt"
func times(x, y int) int {
return x * y
}
func partialTimes(x int) func(int) int {
return func(y int) int {
return times(x, y)
}
}
func main() {
timesTwo := partialTimes(2)
timesThree := partialTimes(3)
timesFour := partialTimes(4)
fmt.Println(timesTwo(5))
fmt.Println(timesThree(5))
fmt.Println(timesFour(5))
}
|
运行这个例子:
1
2
3
4
|
$ go run function_as_first_class_citizen_4.go
10
15
20
|
这里的柯里化是指将原接受两个参数的函数 times 转换为接受一个参数的 partialTimes 的过程。通过 partialTimes 函数构造的 timesTwo 将输入参数扩大为原先 2 倍、timesThree 将输入参数扩大为原先的 3 倍…。
这个例子利用了函数的几点性质:
闭包是前面没有提到的 Go 函数支持的一个特性。 闭包是在函数内部定义的匿名函数,并且允许该匿名函数访问定义它的外部函数的作用域。本质上,闭包是将函数内部和函数外部连接起来的桥梁。
以上述示例来说,partialTimes 内部定义的匿名函数就是一个闭包,该匿名函数访问了其外部函数(partialTimes)的变量 x。这样当调用 partialTimes(2)时,partialTimes 实际上返回一个调用 times(2,y)的函数:
1
2
3
|
timesTwo = func(y int) int {
return times(2, y)
}
|
函子(Functor)
函数式编程范式最让人”望而却步“的就是首先要了解一些抽象概念,比如上面的柯里化,再比如这里的函子(Functor)。什么是函子呢?具体来说,成为函子需要两个条件:
- 函子本身是一个容器类型,以 Go 语言为例,这个容器可以是切片、map 甚至是 channel;
- 光是容器还不够,该容器类型还需要实现一个方法,该方法接受一个函数类型参数,并在容器的每个元素上应用那个函数,得到一个新的函子,原函子容器内部的元素值不受到影响
我们还是用一个具体的示例来直观看一下吧:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
// function_as_first_class_citizen_5.go
package main
import (
"fmt"
)
type IntSliceFunctor interface {
Fmap(fn func(int) int) IntSliceFunctor
}
type intSliceFunctorImpl struct {
ints []int
}
func (isf intSliceFunctorImpl) Fmap(fn func(int) int) IntSliceFunctor {
newInts := make([]int, len(isf.ints))
for i, elt := range isf.ints {
retInt := fn(elt)
newInts[i] = retInt
}
return intSliceFunctorImpl{ints: newInts}
}
func NewIntSliceFunctor(slice []int) IntSliceFunctor {
return intSliceFunctorImpl{ints: slice}
}
func main() {
// 原切片
intSlice := []int{1, 2, 3, 4}
fmt.Printf("init a functor from int slice: %#v\n", intSlice)
f := NewIntSliceFunctor(intSlice)
fmt.Printf("original functor: %+v\n", f)
mapperFunc1 := func(i int) int {
return i + 10
}
mapped1 := f.Fmap(mapperFunc1)
fmt.Printf("mapped functor1: %+v\n", mapped1)
mapperFunc2 := func(i int) int {
return i * 3
}
mapped2 := mapped1.Fmap(mapperFunc2)
fmt.Printf("mapped functor2: %+v\n", mapped2)
fmt.Printf("original functor: %+v\n", f) // 原functor没有改变
fmt.Printf("composite functor: %+v\n", f.Fmap(mapperFunc1).Fmap(mapperFunc2))
}
|
运行这段代码:
1
2
3
4
5
6
7
|
$ go run function_as_first_class_citizen_5.go
init a functor from int slice: []int{1, 2, 3, 4}
original functor: {ints:[1 2 3 4]}
mapped functor1: {ints:[11 12 13 14]}
mapped functor2: {ints:[33 36 39 42]}
original functor: {ints:[1 2 3 4]}
composite functor: {ints:[33 36 39 42]}
|
分析这段代码:
- 这里我们定义了一个 intSliceFunctorImpl 类型,用来作为 functor 的载体;
- 我们把 functor 要实现的方法命名为 Fmap,intSliceFunctorImpl 类型实现了该方法。同时该方法也是 IntSliceFunctor 接口的唯一方法;可以看到在这个代码中真正的 functor 其实是 IntSliceFunctor,这符合 Go 的惯用法;
- 我们定义了创建 IntSliceFunctor 的函数:NewIntSliceFunctor。通过该函数以及一个初始切片,我们可以实例化一个 functor;
- 我们在 main 中定义了两个转换函数,并将这两个函数应用到上述 functor 实例;我们看到得到的新 functor 的内部容器元素值是在原容器的元素值经由转换函数转换后得到的;
- 在最后,我们还可以对最初的 functor 实例连续(组合)应用转换函数,这让我们想到了数学课程中的函数组合;
- 无论如何应用转换函数,原 functor 中容器内的元素值不受到影响。
functor 非常适合对容器集合元素做批量同构处理,而且代码也要比每次都对容器中的元素作循环处理要优雅简洁许多。但要想在 Go 中发挥 functor 的最大效能,还需要 Go 对泛型提供支持,否则我们就需要为每一种容器类型都实现一套对应的 Functor 机制。比如上面的示例仅支持元素类型为 int 的切片,如果元素类型换为 string 或元素类型依然为 int,但容器类型换为 map,我们还需要分别为之编写新的配套代码。
延续传递式(Continuation-passing Style)
函数式编程离不开递归,以求阶乘函数为例,我们可以轻易用递归方法写出一个实现:
1
2
3
4
5
6
7
8
9
10
11
12
|
// function_as_first_class_citizen_6.go
func factorial(n int) int {
if n == 1 {
return 1
} else {
return n * factorial(n-1)
}
}
func main() {
fmt.Printf("%d\n", factorial(5))
}
|
这是一个非常常规的求阶乘的实现思路,函数式编程有一种被称为延续传递式(Continuation-passing Style,以下简称为 CPS)的编程风格.
在 CPS 风格中,函数是不允许有返回值的。一个函数 A 应该将其想返回的值显式传给一个 continuation 函数(一般接受一个参数),而这个 continuation 函数自身是函数 A 的一个参数。概念太过抽象,我们用一个简单的例子来说明一下:
下面得 Max 函数的功能是返回两个参数值中较大的那个值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// function_as_first_class_citizen_7.go
package main
import "fmt"
func Max(n int, m int) int {
if n > m {
return n
} else {
return m
}
}
func main() {
fmt.Printf("%d\n", Max(5, 6))
}
|
我们把 Max 函数看作是上面定义中的 A 函数在未 CPS 化之前的状态。接下来,我们来根据 CPS 的定义将其转换为 CPS 风格:
首先我们去掉 Max 函数的返回值,并为其添加一个函数类型的参数 f(这个 f 就是定义中的 continuation 函数)
1
|
func Max(n int, m int, f func(int))
|
将返回结果传给 continuation 函数,即把 return 语句替换为对 f 函数的调用
1
2
3
4
5
6
7
|
func Max(n int, m int, f func(int)) {
if n > m {
f(n)
} else {
f(m)
}
}
|
完整的转换后的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
// function_as_first_class_citizen_8.go
package main
import "fmt"
func Max(n int, m int, f func(y int)) {
if n > m {
f(n)
} else {
f(m)
}
}
func main() {
Max(5, 6, func(y int) { fmt.Printf("%d\n", y) })
}
|
接下来,我们使用同样的方法将上面的阶乘实现转换为 CPS 风格。
首先我们去掉 factorial 函数的返回值,并为其添加一个函数类型的参数 f(这个 f 也就是 CPS 定义中的 continuation 函数)
1
|
func factorial(n int, f func(y int))
|
接下来,将 factorial 实现中的返回结果传给 continuation 函数,即把 return 语句替换为对 f 函数的调用
1
2
3
4
5
6
7
|
func factorial(n int, f func(int)) {
if n == 1 {
f(n)
} else {
factorial(n-1, func(y int) { f(n *y) })
}
}
|
由于原 else 分支有递归,因此我们需要把未完成的计算过程封装为一个新的函数 f’作为 factorial 递归调用的第二个参数,f’的参数 y 即为原 factorial(n-1)的计算结果,而 n* y 是要传递给 f 的,于是 f’这个函数的定义就为:func(y int) { f(n * y) }。
转换为 CPS 风格的阶乘函数的完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// function_as_first_class_citizen_9.go
package main
import "fmt"
func factorial(n int, f func(int)) {
if n == 1 {
f(1) //基本情况
} else {
factorial(n-1, func(y int) { f(n * y) })
}
}
func main() {
factorial(5, func(y int) { fmt.Printf("%d\n", y) })
}
|
我们简单解析一下上述实例代码的执行过程(下面用伪代码阐释):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
f1 = func(y int) { fmt.Printf("%v\n", y)
factorial(5, f1)
f2 = func(y int) {f1(5 * y)}
factorial(4, f2)
f3 = func(y int) {f2(4 * y)}
factorial(3, f3)
f4 = func(y int) {f3(3 * y)}
factorial(2, f4)
f5 = func(y int) {f4(2 * y)}
factorial(1, f5)
f5(1)
=>
f5(1)
= f4(2 *1)
= f3(3* 2 *1)
= f2(4* 3 *2* 1)
= f1(5 *4* 3 *2* 1)
= 120
|
读到这里很多朋友会提出心中的疑问:这种 CPS 风格虽然利用了函数作为”一等公民“的特质,但是其代码理解起来颇为困难,这种风格真的好吗?朋友们的担心是有道理的。这里对 CPS 风格的讲解其实是一个”反例“,目的就是告诉大家,尽管作为”一等公民“的函数给 Go 带来的强大的表达能力,但是如果选择了不适合的风格或者说为了函数式而进行函数式编程,那么就会出现代码难于理解,且代码执行效率不高的情况(CPS 需要语言支持尾递归优化,但 Go 目前并不支持)。
尾递归优化
我们知道函数调用底层是通过栈来维护的,对于递归函数而言,如果层级太深,同时保存成百上千的调用记录,会导致这个栈越来越大,消耗大量内存空间,严重情况下会导致栈溢出(stack overflow),为了优化这个问题,可以引入尾递归优化技术来重用栈,降低对内存空间的消耗,提升递归函数性能。
尾递归优化是函数式编程的重要特性之一,在了解尾递归优化前,我们先来看看什么是尾递归。
在计算机科学里,尾调用是指一个函数的最后一个动作是调用一个函数(只能是一个函数调用,不能有其他操作,比如函数相加、乘以常量等):
1
2
3
4
|
func f(x int) int {
...
return g(x);
}
|
这种情况下称该调用位置为尾位置,若这个函数在尾位置调用自身,则称这种情况为尾递归,它是尾调用的一种特殊情形。尾调用的一个重要特性是它不是在函数调用栈上添加一个新的堆栈帧 —— 而是更新它,尾递归自然也继承了这一特性,这就使得原来层层递进的调用栈变成了线性结构,因而可以极大优化内存占用,提升程序性能,这就是尾递归优化技术。
一些编程语言的编译器提供了对尾递归优化的支持,但是 Go 目前并不支持,为了使用尾递归优化技术,需要手动编写实现代码。
尾递归的实现需要重构之前的递归函数,确保最后一步只调用自身,要做到这一点,就要把所有用到的内部变量/中间状态变成函数参数.
以 fibonacci 函数为例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
package main
import (
"fmt"
"time"
)
type FibonacciFunc func(int) int
// 通过递归函数实现斐波那契数列
func fibonacci(n int) int {
// 终止条件
if n == 1 {
return 0
}
if n == 2 {
return 1
}
// 递归公式
return fibonacci(n-1) + fibonacci(n-2)
}
// 斐波那契函数执行耗时计算
func fibonacciExecTime(f FibonacciFunc) FibonacciFunc {
return func(n int) int {
start := time.Now() // 起始时间
num := f(n) // 执行斐波那契函数
end := time.Since(start) // 函数执行完毕耗时
fmt.Printf("--- 执行耗时: %v ---\n", end)
return num // 返回计算结果
}
}
func main() {
n1 := 5
f := fibonacciExecTime(fibonacci)
r1 := f(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
}
|
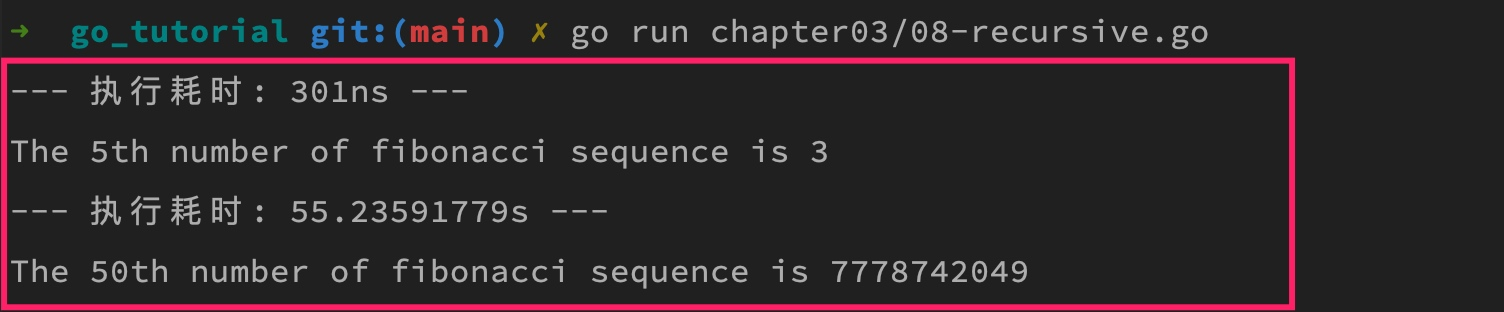
可以看到,虽然 5 和 50 从序号上看只相差了 10 倍,但是最终体现在递归函数的执行时间上,却是不止十倍百倍的巨大差别(1s = 10亿ns)。
究其原因,一方面是因为递归函数调用产生的额外开销,另一方面是因为目前这种实现存在着重复计算,比如我在计算 fibonacci(50) 时,会转化为计算 fibonacci(49) 与 fibonacci(48) 之和,然后我在计算 fibonacci(49) 时,又会转化为调用 fibonacci(48) 与 fibonacci(47) 之和,这样一来 fibonacci(48) 就会两次重复计算,这一重复计算就是一次新的递归(从序号 48 递归到序号 1),以此类推,大量的重复递归计算堆积,最终导致程序执行缓慢。
我们先对后一个原因进行优化,通过缓存中间计算结果来避免重复计算,从而提升递归函数的性能。
按照这个思路我们来重写下递归函数 fibonacci 的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
const MAX = 50
var fibs [MAX]int
// 缓存中间结果的递归函数优化版
func fibonacci2(n int) int {
if n == 1 {
return 0
}
if n == 2 {
return 1
}
index := n - 1
if fibs[index] != 0 {
return fibs[index]
}
num := fibonacci2(n-1) + fibonacci2(n-2)
fibs[index] = num
return num
}
|
这一次,我们会通过预定义数组 fibs 保存已经计算过的斐波那契序号对应的数值(序号 n 与对应数组索引的映射关系为 n-1,因为数组索引从下标 0 开始,而这里的斐波那契序号从 1 开始),这样下次要获取对应序号的斐波那契值时会直接返回而不是调用一次递归函数进行计算。
将调用代码调整如下:
1
2
3
4
5
6
7
8
9
10
11
12
|
func main() {
n1 := 5
f1 := fibonacciExecTime(fibonacci)
r1 := f1(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f1(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
f2 := fibonacciExecTime(fibonacci2)
r3 := f2(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r3)
}
|
再次执行,通过打印结果耗时对比可以看出,之前执行慢主要是重复的递归计算导致的(1µs=1000ns,所以其性能和 fibonacci(5) 是在一个数量级上):
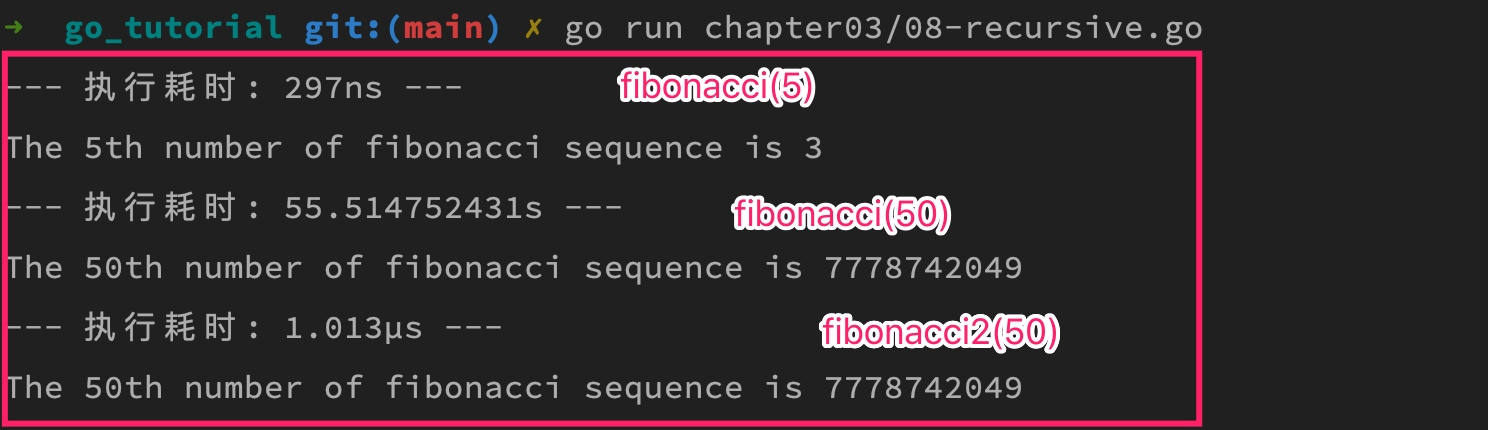
这种优化是在内存中保存中间结果,所以称之为内存缓存技术(memoization),这种内存缓存技术在优化计算成本相对昂贵的函数调用时非常有用。
接下来,我们来看能否对造成上述递归函数性能低下的第一个原因进行优化。
简单来说,就是处于函数尾部的递归调用前面的中间状态都不需要再保存了,这可以节省很大的内存空间,在此之前的代码实现中,递归调用 fibonacci(n-1) 时,还有 fibonacci(n-2) 没有执行,因此需要保存前面的中间状态,内存开销很大。我们可以这样实现尾递归函数 fibonacciTail:
1
2
3
4
5
6
|
func fibonacciTail(n, first, second int) int {
if n < 2 {
return first
}
return fibonacciTail(n-1, second, first+second)
}
|
当前 first + second 的和赋值给下次调用的 second 参数,当前 second 值赋值给下次调用的 first 参数,就等同于实现了 F(n) = F(n-1) + F(n-2) 的效果,循环往复,不断累加,直到 n 值等于 1(F(1) = 0,无需继续迭代下去),则返回 first 的值,也就是最终的 F(n) 的值。
简单来说,就是把原来通过递归调用计算结果转化为通过外部传递参数初始化,再传递给下次尾递归调用不断累加,这样就可以保证 fibonacciTail 调用始终是线性结构的更新,不需要开辟新的堆栈保存中间函数调用。
但是从语义上看这个新的斐波那契函数有点怪,我们可以在外面套一层:
1
2
3
|
func fibonacci3(n int) int {
return fibonacciTail(n, 0, 1) // F(1) = 0, F(2) = 1
}
|
这样,就可以像之前一样调用 fibonacci3 计算在斐波那契数列中序号 n 的值了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func main() {
n1 := 5
f1 := fibonacciExecTime(fibonacci)
r1 := f1(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f1(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
f2 := fibonacciExecTime(fibonacci2)
r3 := f2(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r3)
f3 := fibonacciExecTime(fibonacci3)
r4 := f3(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r4)
}
|
执行上述代码,打印结果如下:
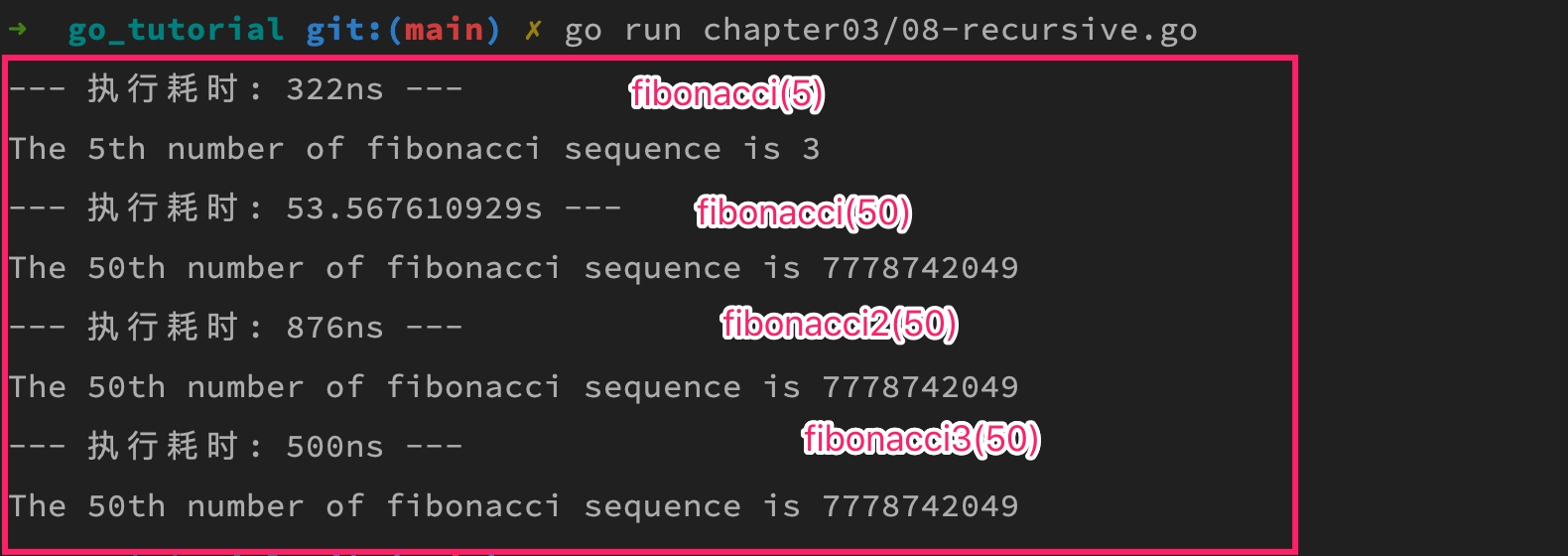
可以看到,尾递归优化版递归函数性能要优于内存缓存技术优化版,并且不需要借助额外的内存空间保存中间结果,因此从性能角度看是更好的选择,就是可读性差一些,理解起来有些困难。
延迟计算 Delayed Calculating
使用高阶/匿名函数的一个重要用途是捕俘变量和延迟计算,也即所谓的惰性计算(Lazy evaluations)。
在下面这个例子中,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func doSth(){
var err error
defer func(){
if err != nil {
println(err.Error())
}
}()
// ...
err = io.EOF
return
}
doSth() // printed: EOF
|
在 defer 的高阶函数中,捕俘了外部作用域中的 err 变量,doSth 的整个运行周期中对 err 的设定,最终能够在 defer 函数体中被正确计算得到。如果没有捕俘和延迟计算机制的话,高阶函数体中对 err 的访问就只会得到 nil 值,因为这是捕俘时刻 err 的具体值。请注意为了缩减示例代码规模我们采用了 defer 来演示,实际上使用 go routines 可以得到同样的效果,换句话说,在高阶函数中对外部作用域的访问是动态地延迟地计算的。
选项模式
作为一个类库作者,迟早会面临到接口变更问题。或者是因为外部环境变化,或者是因为功能升级而扩大了外延,或者是因为需要废弃掉过去的不完善的设计,或者是因为个人水平的提升,无论哪一种理由,你都可能会发现必须要修改掉原有的接口,替换之以一个更完美的新接口。
想象下有一个早期的类库:
1
2
3
4
5
6
7
8
9
10
11
|
package tut
func New(a int) *Holder {
return &Holder{
a: a,
}
}
type Holder struct {
a int
}
|
后来,我们发现需要增加一个布尔量 b,于是修改 tut 库为:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
package tut
func New(a int, b bool) *Holder {
return &Holder{
a: a,
b: b,
}
}
type Holder struct {
a int
b bool
}
|
没过几天,现在我们认为有必要增加一个字符串变量,tut 库不得不被修改为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
package tut
func New(a int, b bool, c string) *Holder {
return &Holder{
a: a,
b: b,
c: c,
}
}
type Holder struct {
a int
b bool
c string
}
|
想象一下,tut 库的使用者在面对三次接口 New() 的升级时,会有多少 MMP 要抛出来。
对此我们需要 选项模式 来解救之。
假设 tut 的第一版我们是这样实现的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
package tut
type Opt func (holder *Holder)
func New(opts ...Opt) *Holder {
h := &Holder{ a: -1, }
for _, opt := range opts {
opt(h)
}
return h
}
func WithA(a int) Opt {
return func (holder *Holder) {
holder.a = a
}
}
type Holder struct {
a int
}
//...
// You can:
func vv(){
holder := tut.New(tut.WithA(1))
// ...
}
|
同样地需求变更发生后,我们将 b 和 c 增加到现有版本上,那么现在的 tut 看起来是这样的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
package tut
type Opt func (holder *Holder)
func New(opts ...Opt) *Holder {
h := &Holder{ a: -1, }
for _, opt := range opts {
opt(h)
}
return h
}
func WithA(a int) Opt {
return func (holder *Holder) {
holder.a = a
}
}
func WithB(b bool) Opt {
return func (holder *Holder) {
holder.b = b
}
}
func WithC(c string) Opt {
return func (holder *Holder) {
holder.c = c
}
}
type Holder struct {
a int
b bool
c string
}
//...
// You can:
func vv(){
holder := tut.New(tut.WithA(1), tut.WithB(true), tut.WithC("hello"))
// ...
}
|
由于代码没有什么复杂度,所以我不必逐行解说实例代码了。你将会得到一个直观的感受是,原有的 tut 的用户端遗留代码(例如 vv() )实际上可以完全不变,透明地应对 tut 库本身的升级动作。
这里要提到这种编码范式的特点和作用包括:
a. 在实例化 Holder 时,我们现在可以变相地使用不同数据类型的任意多可变参数了。
b. 借助既有的范式模型,我们还可以实现任意的复杂的初始化操作,用以为 Holder 进行不同的构建操作。
c. 既然是范式,那么其可读性、可拓展性需要被研究——很明显,现在的这一范式能得到高分。
d. 在大版本升级时,New(…) 的接口稳固性相当好,无论你如何调整内在算法及其实现,对这样的第三方库的调用者来说,没有什么需要改变的。
参考
使用 Go 泛型的函数式编程
Golang 函数式编程简述
Go 函数是“一等公民”的理解
Go 函数式编程篇(四):通过高阶函数实现装饰器模式
Go 函数式编程篇(五):递归函数及性能调优


