转载： http://www.cnblogs.com/QG-whz/p/5167238.html. http://blog.csdn.net/sp_programmer/article/details/41812787.

定义

AVL树又称为高度平衡的二叉搜索树。它能保持二叉树的高度平衡，尽量降低二叉树的高度，减少树的平均搜索长度。

性质

AVL树本质上还是一棵二叉搜索树（因此读者可以看到我后面的代码是继承自二叉搜索树的），它的特点是：

本身首先是一棵二叉搜索树。
带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

例如：

    5              5
   / \            / \
  2   6          2   6
 / \   \        / \
1   4   7      1   4
   /              /
  3              3

上图中，左边的是AVL树，而右边的不是。因为左边的树的每个结点的左右子树的高度之差的绝对值都最多为1，而右边的树由于结点6没有子树，导致根结点5的平衡因子为2。

效率

一棵AVL树有N个节点，其高度可以保持在lgN，插入/删除/查找的时间复杂度也是lgN。

我们先来看看二叉搜索树吧（因为AVL树本质上是一棵二叉搜索树），假设有这么一种极端的情况：二叉搜索树的结点为1、2、3、4、5，也就是：

这棵二叉搜索树其实等同于一个链表了，也就是说，它在查找上的优势已经全无了——在这种情况下，查找一个结点的时间复杂度是O(N)！

好，那么假如是AVL树（别忘了AVL树还是二叉搜索树），则会是：

可以看出，AVL树的查找平均时间复杂度要比二叉搜索树低——它是O(logN)，但是插入操作可能会破坏平衡性另当别论了，也正是我们下面只讨论插入操作的原因。也就是说，在大量的随机数据中AVL树的表现要好得多。

节点结构

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


struct AVLTreeNode
{
    AVLTreeNode(T value, AVLTreeNode<T>*l, AVLTreeNode<T>*r)
    :key(value), lchild(l), rchild(r){}

    T key;
    int height;		//节点的高度，用于计算父节点的平衡因子
    AVLTreeNode<T>* lchild;
    AVLTreeNode<T>* rchild;
};

旋转操作

假设有一个结点的平衡因子为2（在AVL树中，最大就是2，因为结点是一个一个地插入到树中的，一旦出现不平衡的状态就会立即进行调整，因此平衡因子最大不可能超过2），那么就需要进行调整。由于任意一个结点最多只有两个儿子，所以当高度不平衡时，只可能是以下四种情况造成的：

对该结点的左儿子的左子树进行了一次插入。
对该结点的左儿子的右子树进行了一次插入。
对该结点的右儿子的左子树进行了一次插入。
对该结点的右儿子的右子树进行了一次插入。

情况1和4是关于该点的镜像对称，同样，情况2和3也是一对镜像对称。因此，理论上只有两种情况，当然了，从编程的角度来看还是四种情况。

第一种情况是插入发生在“外边”的情况（即左-左的情况或右-右的情况），该情况可以通过对树的一次单旋转来完成调整。第二种情况是插入发生在“内部”的情况（即左-右的情况或右-左的情况），该情况要通过稍微复杂些的双旋转来处理。注意所有旋转情况都是围绕着使得二叉树不平衡的第一个节点展开的。

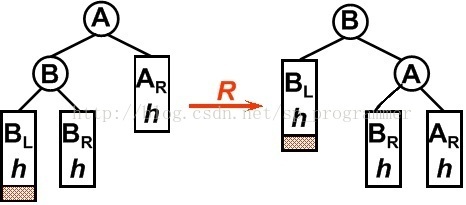
1. LL型

平衡二叉树某一节点的左孩子的左子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向右旋转一次即可，如图所示，原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


/*右旋转操作*/
/*pnode为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template <typename  T>
AVLTreeNode<T>* AVLTree<T>::rightRotation(AVLTreeNode<T>*proot)
{
    AVLTreeNode<T>* plchild = proot->lchild;
    proot->lchild = plchild->rchild;
    plchild->rchild = proot;

    proot->height = max(height(proot->lchild), height(proot->rchild)) + 1;     //更新节点的高度值
    plchild->height = max(height(plchild->lchild), height(plchild->rchild)) + 1; //更新节点的高度值

    return plchild;
};

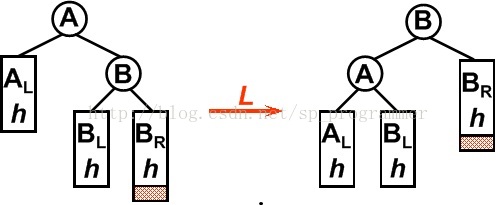
2. RR型

平衡二叉树某一节点的右孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时只需要把树向左旋转一次即可，如图所示，原A右孩子B变为父结点，A变为其左孩子，而原B的左子树Blh将变为A的右子树。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


/*左旋转操作*/
/*pnode为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template<typename T>
AVLTreeNode<T>* AVLTree<T>::leftRotation(AVLTreeNode<T>* proot)
{
    AVLTreeNode<T>* prchild = proot->rchild;
    proot->rchild = prchild->lchild;
    prchild->lchild = proot;

    proot->height = max(height(proot->lchild),height(proot->rchild))+1;     //更新节点的高度值
    prchild->height = max(height(prchild->lchild), height(prchild->rchild)) + 1; //更新节点的高度值

    return prchild;
};

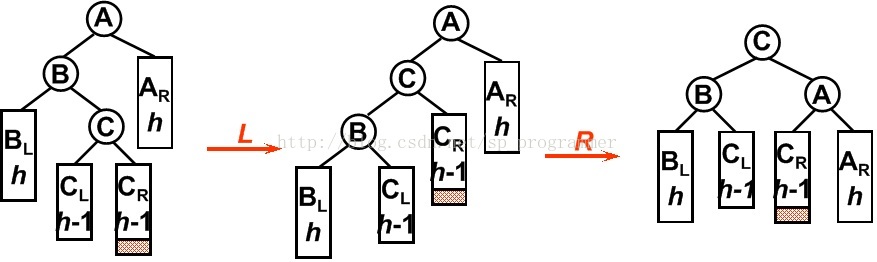
3. LR型

平衡二叉树某一节点的左孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时需要旋转两次，仅一次的旋转是不能够使二叉树再次平衡。如图所示，在B节点按照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还需要再向右旋转一次。

1
2
3
4
5
6
7
8
9


/*先左后右做旋转*/
/*参数proot为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template <typename T>
AVLTreeNode<T>* AVLTree<T>::leftRightRotation(AVLTreeNode<T>* proot)
{
    proot->lchild= leftRotation(proot->lchild);
    return rightRotation(proot);
};

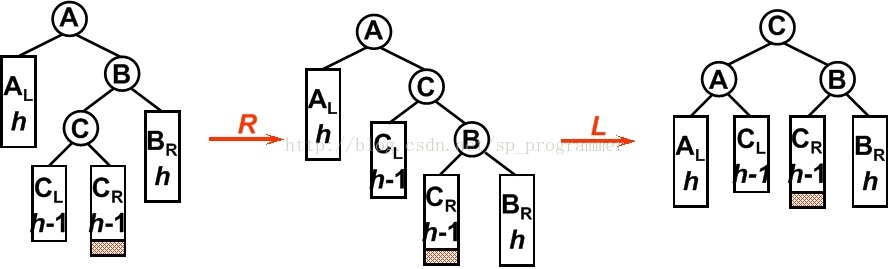
4. RL型

平衡二叉树某一节点的右孩子的左子树上插入一个新的节点，使得该节点不再平衡。同样，这时需要旋转两次，旋转方向刚好同LR型相反。

1
2
3
4
5
6
7
8
9


/*先右旋再左旋*/
/*参数proot为最小失衡子树的根节点*/
/*返回旋转后的根节点*/
template<typename T>
AVLTreeNode<T>* AVLTree<T>::rightLeftRotation(AVLTreeNode<T>* proot)
{
    proot->rchild = rightRotation(proot->rchild);
    return leftRotation(proot);
};

插入操作

插入的核心思路是通过递归找到合适的位置，插入新结点，然后看新结点是否平衡（平衡因子是否为2），如果不平衡的话，就分成三种大情况以及两种小情况：

在结点的左儿子(X < T->item)
1. 在左儿子的左子树 (X < T->l-> item)，“外边”，要做单旋转。
2. 在左儿子的右子树 (X > T->l-> item)，“内部”，要做双旋转。
在结点的右儿子(X > T->item)
1. 在右儿子的左子树(X < T->r-> item)，“内部”，要做双旋转。
2. 在右儿子的右子树(X > T->r-> item)，“外边”，要做单旋转。
(X == T->item) ，对该节点的计数进行更新。实现代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


/*插入操作*/
/*递归地进行插入*/
/*返回插入后的根节点*/
template <typename T>
AVLTreeNode<T>* AVLTree<T>::insert(AVLTreeNode<T>* &pnode, T key)
{
    if (pnode == nullptr)    //寻找到插入的位置
    {
        pnode = new AVLTreeNode<T>(key, nullptr, nullptr);
    }
    else if (key > pnode->key)    //插入值比当前结点值大，插入到当前结点的右子树上
    {
        pnode->rchild = insert(pnode->rchild, key);
        if (height(pnode->rchild) - height(pnode->lchild) == 2) //插入后出现失衡
        {
            if (key > pnode->rchild->key) //情况一：插入右子树的右节点，进行左旋
                pnode=leftRotation(pnode);
            else if (key < pnode->rchild->key)  //情况三：插入右子树的左节点,进行先右再左旋转
                pnode=rightLeftRotation(pnode);
        }
    }
    else if (key < pnode->key) //插入值比当前节点值小，插入到当前结点的左子树上
    {
        pnode->lchild = insert(pnode->lchild, key);
        if (height(pnode->lchild) - height(pnode->rchild) == 2) //如果插入导致失衡
        {
            if (key < pnode->lchild->key)        //情况二：插入到左子树的左孩子节点上，进行右旋
                pnode = rightRotation(pnode);
            else if (key>pnode->lchild->key)
                pnode = leftRightRotation(pnode);//情况四：插入到左子树的右孩子节点上，进行先左后右旋转
        }
    }
    pnode->height = max(height(pnode->lchild), height(pnode->rchild)) + 1;
    return pnode;
};

删除操作

删除节点也可能导致AVL树的失衡，实际上删除节点和插入节点是一种互逆的操作：

删除右子树的节点导致AVL树失衡时，相当于在左子树插入节点导致AVL树失衡。

删除左子树的节点导致AVL树失衡时，相当于在右子树插入节点导致AVL树失衡。

另外，AVL树也是一棵二叉排序树，因此在删除节点时也要维护二叉排序树的性质。

删除节点有三种情况分析：

叶子节点；(直接删除即可)

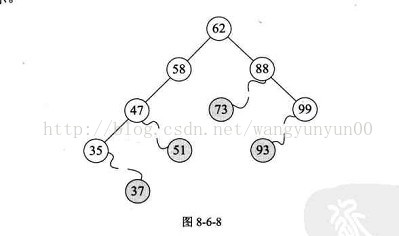
仅有左或右子树的节点；（上移子树即可）

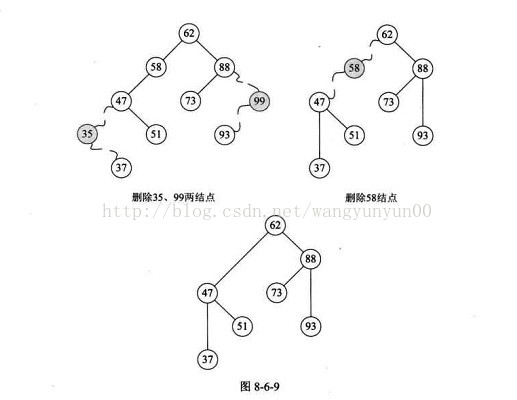
左右子树都有的节点。可以用删除节点在中序遍历时的直接前驱或者直接后继来替换当前节点，然后删除直接前驱或者直接后继的原位置。

如果从左子树中选，就应该选择左子树中最右边的那个叶子节点
如果从右子树中选，就应该选择有子树中最左边的那个叶子节点。

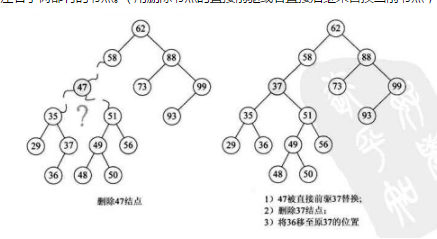
因为是在AVL树上进行删除，所以在高度较低的子树上选择最大（或最小）元素进行替换，这样能保证替换后不会再出现失衡的现象。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70


/*删除指定元素*/
template<typename T>
AVLTreeNode<T>* AVLTree<T>::remove(AVLTreeNode<T>* & pnode, T key)
{
    if (pnode != nullptr)
    {
        if (key == pnode->key)            //找到删除的节点
        {
            //因AVL也是二叉排序树，删除节点要维护其二叉排序树的条件
            if (pnode->lchild != nullptr&&pnode->rchild != nullptr)        //若左右都不为空
            {
                // 左子树比右子树高,在左子树上选择节点进行替换
                if (height(pnode->lchild) > height(pnode->rchild))
                {
                    //使用左子树最大节点来代替被删节点，而删除该最大节点
                    AVLTreeNode<T>* ppre = maximum(pnode->lchild);        //左子树最大节点
                    pnode->key = ppre->key;                                //将最大节点的值覆盖当前结点
                    pnode->lchild = remove(pnode->lchild, ppre->key);    //递归地删除最大节点
                }
                else  //在右子树上选择节点进行替换
                {
                    //使用最小节点来代替被删节点，而删除该最小节点
                    AVLTreeNode<T>* psuc = minimum(pnode->rchild);        //右子树的最小节点
                    pnode->key = psuc->key;                                //将最小节点值覆盖当前结点
                    pnode->rchild = remove(pnode->rchild, psuc->key);    //递归地删除最小节点
                }

            }
            else	//至多有一个子树，上移子树或直接删除
            {
                AVLTreeNode<T> * ptemp = pnode;
                if (pnode->lchild != nullptr)
                    pnode = pnode->lchild;
                else if (pnode->rchild != nullptr)
                    pnode = pnode->rchild;
                delete ptemp;
                return nullptr;
            }

        }
        else if (key > pnode->key)//要删除的节点比当前节点大，则在右子树进行删除
        {
            pnode->rchild =  remove(pnode->rchild, key);
            //删除右子树节点导致不平衡:相当于增加左子树节点
            if (height(pnode->lchild) - height(pnode->rchild) == 2)
            {
                //相当于在左子树上插入右节点造成的失衡（LR）
                if (height(pnode->lchild->rchild)>height(pnode->lchild->lchild))
                    pnode = leftRightRotation(pnode);
                else//相当于在左子树上插入左节点造成的失衡（LL）
                    pnode = rightRotation(pnode);
            }
        }
        else if (key < pnode->key)//要删除的节点比当前节点小，则在左子树进行删除
        {
            pnode->lchild= remove(pnode->lchild, key);
             //删除左子树节点导致不平衡：相当于增加右子树节点
            if (height(pnode->rchild) - height(pnode->lchild) == 2)
            {
                //相当于在右子树上插入左节点造成的失衡（RL）
                if (height(pnode->rchild->lchild)>height(pnode->rchild->rchild))
                    pnode = rightLeftRotation(pnode);
                else//相当于在右子树上插入右节点造成的失衡（RR）
                    pnode = leftRotation(pnode);
            }
        }
        return pnode;
    }
    return nullptr;
};

AVL树详解

文章目录

定义

性质

效率