线性同余法与伪随机数
文章目录
公式定义
在离散数据及其应用中,如果
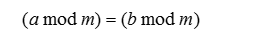
那么,称a模m同余b(或者称模m时,a等价于b),可以记为
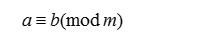
而线性同余式就可以这样表示:
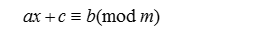
线性同余发生器与上面的线性同余式多少有一些关系。
按照The Art of Computer Programming,Volume 2[1]中3.21. The Linear Congruential Method的思路,线性同余发生器(LCG:Linear Congruential Generators )可以采用如下公式化定义:

其中:
模数m和系数a是这个公式中最重要的参数,如何合理的选择这两个参数决定了其产生的线性同余序列(LCS:Linear Congruential Scquence):质量的优劣($X_1$,$X_2$,$X_3$..$X_n$…)。
常数c可以为0,也可以不为0。通常,如果c=0,那么(2)式也称作乘法线性同余发生器(MCG:Multiplicative Congruential Generator),如果c非0,(2)式,则称作混合线性同余发生器(Mixed Linear Congruential Generator)。
$X_0$称作初始值,也就是所谓的种子seed。
线性同余序列的周期
如上的线性同余发生器产生的线性同余序列必然会存在一个周期P。在TAOCP中,作者以一个练习的方式提出了这个问题(exercise 3.1-6)。以下通过一种简单直白但不严谨的推理来解释这个问题。
将上述线性同余公式抽象为一个函数f(将$X_n$映射为$X_{n+1}$),这个函数具有自封闭特性。不难发现,实际上存在以下已知条件:
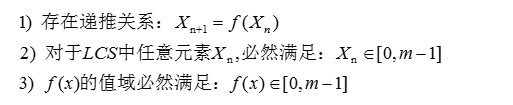
定义两个集合:S和T。初始状态下,集合S包含了从0到m-1所有的m个元素,集合T是一个空集。
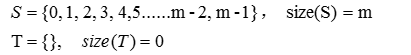
现模拟产生LCS的过程,以任意值$X_0$为参数,产生第一个伪随机数$X_1$。其值必然属于集合S,此时将$X_1$从集合S移动到集合T。
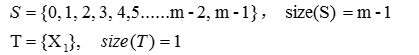
以$X_1$为参数,产生第二个伪随机数$X_2$=f($X_1$),此时,$X_2$有可能属于集合S,也有可能属于集合T。
-
如果$X_2$属于集合S,那么此时还没有产生一个周期;
-
如果$X_2$属于集合T,此处也就是刚好等于$X_1$,那么此时一个周期产生,周期P=1。
更一般地,假设在生成$X_1$到$X_{i-1}$过程中,每个数都是在集合S中找到的,则每个数都从集合S中移动到了集合T,此时两个集合的状态为:
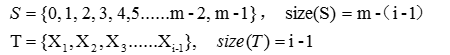
然后生成$X_i$时,
-
如果$X_i$=f($X_{i-1}$)在集合S中,则未能产生一个周期;
-
如果$X_i$=f($X_{i-1}$)在集合T中,则一个周期产生,此时周期P<=i-1。
当然周期P也有可能等于m,也就是集合S最终为空集,集合T容纳了0到m-1的所有元素,且f(Xm)=$X_1$。
因此,从以上推理不难得知,LCS必然存在一个周期P,且P<=m。
进而不难推断:
-
如果某LCG产生的随机序列的周期P小于m,则选取不同的初始值$X_0$产生的LCS可能有不同的周期。
-
如果其周期P=m,则即使选取不同的$X_0$,产生的这些LCS具有相同的周期且必定为P。
例如,对于下面发生器:
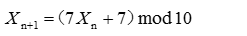
如果以初始值$X_0$=12产生随机序列为:
|
|
如果以初始值$X_0$=13产生随机序列则为:
|
|
但是,对于如下的发生器:
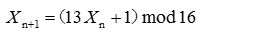
无论选取何值为种子产生的随机序列,其周期都是16。
关于参数选择
构造一个表现良好的线性同余发生器并非易事,不但考虑其产生的随机序列的周期、随机分布特点,还要考虑计算的效率。
在参数的选择方面,最关键的就是m和a的选择。
m 选择
m应该尽可能大,这样才有可能产生较长的周期。如果计算机的字长为w位,TAOCP中推荐,应该取m=2^w,或者m=2^w+1,或者m=2^w-1,也可以取小于2^w的最大的素数,在论文TABLES OF LINEAR CONGRUENTIAL GENERATORS OF DIFFERENT SIZES AND GOOD LATTICE STRUCTURE[2] 中就采用了这种m值选取的方式。
通常而言,如果取m=2^w,则利用位运算往往会使计算过程更加方便和高效,但是会存在一个问题:产生的随机序列中各元素的低比特位的随机性并不是很好。
简单的解释是,当m=2^w时,对于一个s位的整数Z,Z模m的结果实际上就是Z的比特位中右边的s-w位的结果。
作者在原文中用了比较形式化的描述来说明这个问题:
假设d是m的一个因子,q为某一整数,令Yn满足如下关系:
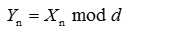
然后进行如下变换:
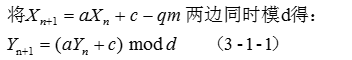
不难发现由公式3-1-1实际就是一个线性同余发生器,产生的随机序列也具有周期,但是其周期小于等于d。
这里的<Y>序列实际上对应了原线性同余序列<X>的低位字节,可以将序列<Y>理解为是将<X>的低位单独抽取出来组成的一个序列。例如如果d=2^4, 则序列的周期最大也就是16,对应了序列中各个元素的低4位比特位的周期最大是16,显然低位的随机性并不是很好。正是由于这个原因,有些平台的实现会丢弃这些随机性不好的低比特位,截取高比特位以取得一个比较好的随机性效果。大多数应用场景中,低比特位并不会对最终用途产生影响,因此选取m=2^w 基本能够满足要求,实际上很多平台也确实都是取m=2^w。
如果m取2^w +1或者m=2^w -1,则不会产生上述问题。
a 选择
a的选择推理过程比较复杂一些。一般来讲,应该使LCS的周期尽量长(最长为m),然后只使用一个周期内的元素,但是周期长的序列可能并不具有很好的随机性。
比如如下的线性同余发生器:
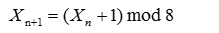
以初始值$X_0$=3产生随机序列的结果:
|
|
可见,以上序列的随机性表现很糟糕。
在TAOCP中证明了如下定理,按照如下方式来选定系数a可以产生最大周期为m的LCS。

以上定理表明当c不等0时(c与m互质当然就不可能等于0),有可能产生周期为m的LCS。
另一方面,当c=0时,也即:
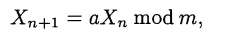
是否也有可能产生周期为m的LCS呢?答案是必然不可能。
一个简单的反证法:
如果c=0时,产生了周期为m的LCS,那么0必然在这个序列中,但是如果0在序列中,必然会导致LCS退化成全0的序列,因此原命题必然不成立。
从另一个角度考虑:
考虑d是m的一个因子,且$X_n$是d的倍数,也即$X_n$=kd,其中k为某整数。于是有如下推导:
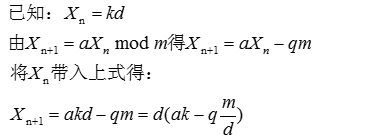
由此可知,$X_n$+1也是d的倍数,同理,后面的$X_n$+2,$X_n$+2也是d的倍数,现在这样的序列也不是一个号的序列。所以如果要求序列中各个元素分别与m形成互质关系,因此这样的序列的元素个数实际就是欧拉函数对m求值,也即:
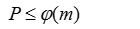
总结
简单总结几点即是:
-
模数m应该尽可能大,通常至少大于2^30,为了计算效率,通常会结合计算机的字长考虑选取m的值。m值直接影响伪随机数序列的周期长短。
-
如果m选取为2的幂,也即m=2^w,则选取的a通常应该满足a模8等于5。当a=1的时候,Xn=(X0+nc)mod m ,它不具有随机序列的特性;而当a=0的时候甚至更糟糕。因此,为实用起见,选择2 <= a< m比较合理。乘数a最好满足a=4p+1;
-
当参数m和a的选定比较合理时,对于c的选择约束性不是很强烈,但要保证c与m互质。例如c可以选择1或者11。当c=0时,数的生成过程比c!=0的时候要稍微快些,它的限制缩短了这个序列的周期长度,但是也仍然有可能得到一个相当长的周期。当c=0时被称为乘同余法,c!=0称为混合同余法。为了一般性,我建议选择采用混合同余法。增量c满足b=2q+1。其中p,q都是正整数。
-
种子seed应该是随机选取的,可以将时间戳作为种子。
-
a和c值越大,产生的伪随机数越均匀。
-
a和m互质,产生的随机数效果较不互质好。
因为$X_n$的低有效位的随机性表现并不是很好,所以在对$X_n$的随机特性比较敏感的应用场景中,应该尽量采用高比特位。事实上,更应该将值$X_n$/m视为0到1之间的均匀分布,而不是直接将$X_n$视为0到m-1之间的均匀分布。所以,如果希望产生0到k-1之间的均匀分布伪随机数,应该采用k$X_n$/m的方式。
MCG
当LCG的c = 0,它被称为multiplier congruence generator(MCG). 这种情况下不可能达到满周期,即周期一定小于M。且种子不能为0(也不能是M、2M、3M…),否则得到的序列将是全zero。
在MCG中,若a是M的Primitive Root,则此MCG的周期等于T-1。一个具体的例子,当M=2^31 − 1,则M具有以下Primitive Root: 16807, 397204094, 764261123, 630360016. 就我目前看过的代码中, 选16807的居多.
因为 M = 2^31 − 1 = 2147483647 = 127773 * 16807 + 2836
我们可以用127773把seed分成高位和低位两部分.
seed = hi* 127773 + lo ;
所以 seed * 16807 = hi* 127773 * 16807 + lo * 16807 = hi * (M - 2836) + lo * 16807
上式最右端对M取余后得到 lo * 16807 - hi * 2836
但是这个计算结果有可能是负数, 此时让它加上M. 就回到[0,M)的范围内了.
但是这个技巧其实并不高明. 因为把seed拆成hi和lo两部分的时候, 需要计算除法. 而在现代CPU上, 除法的代价是乘法的10-30倍, 很可怕.
注意,multiplier congruence generator(c=0)生成的是[1,M - 1]上的均匀分布。所以一般来说会把它减去1后再返回,这样得到的就是[0, M-2]上的均匀分布. 假如你拿它做随机抽样, 结果数组中第一个元素永远也抽不中.
参考: https://www.cnblogs.com/qcblog/p/8450427.html https://blog.csdn.net/orchidzouqr/article/details/53139220 http://www.voidcn.com/article/p-kprhvxyq-pn.html
文章作者 Forz
上次更新 2019-10-09