快速幂

题目:Implement pow(x, n).

解析：快速幂，此处需要判断边界值n，如果n为-2^31，那么需要另外设置一个long long变量存储其相反数。0x80000000（10000000000000000000000000000000），计算机在表示INT_MIN的时候，将符号位和数值位混用，使得INT_MIN比INT_MAX的绝对值大1，而且无法在INT范围内取相反数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    double myPow(double x, int n) {
        long long m=n;//
        if(m<0){
            m=-m;
            x=1.0/x;
        }
        double ans=1;
        while(m){//利用二进制形式快速幂
            if(m&1) ans=ans*x;
            x=x*x;//底数直接乘方
            m>>=1;//不能使用n>>=1,因为n可能是-2147483648 = -2^31
        }
        return ans;
    }
};

矩阵乘法原理

矩阵的本质就是线性方程式，两者是一一对应关系。如果从线性方程式的角度，理解矩阵乘法就毫无难度。

下面是一组线性方程式。

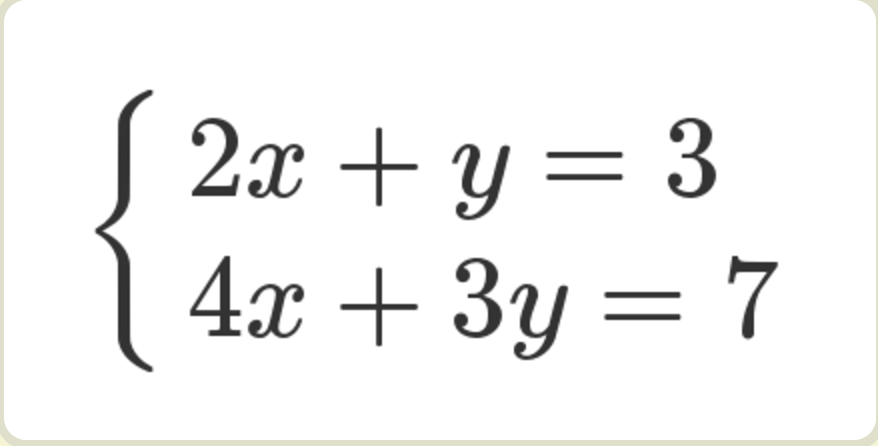
矩阵的最初目的，只是为线性方程组提供一个简写形式。

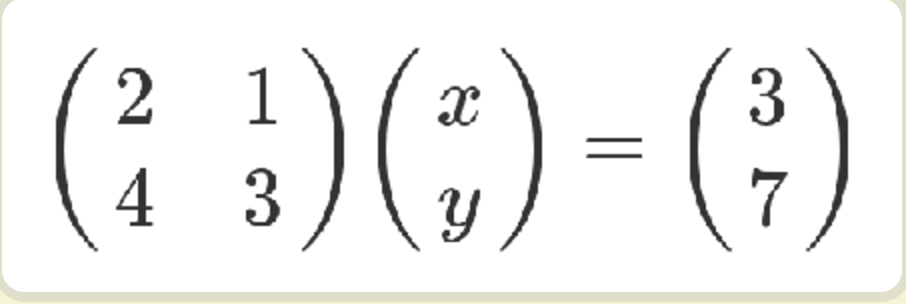
老实说，从上面这种写法，已经能看出矩阵乘法的规则了：系数矩阵第一行的2和1，各自与 x 和 y 的乘积之和，等于3。不过，这不算严格的证明，只是线性方程式转为矩阵的书写规则。

下面才是严格的证明。有三组未知数 x、y 和 t，其中 x 和 y 的关系如下。

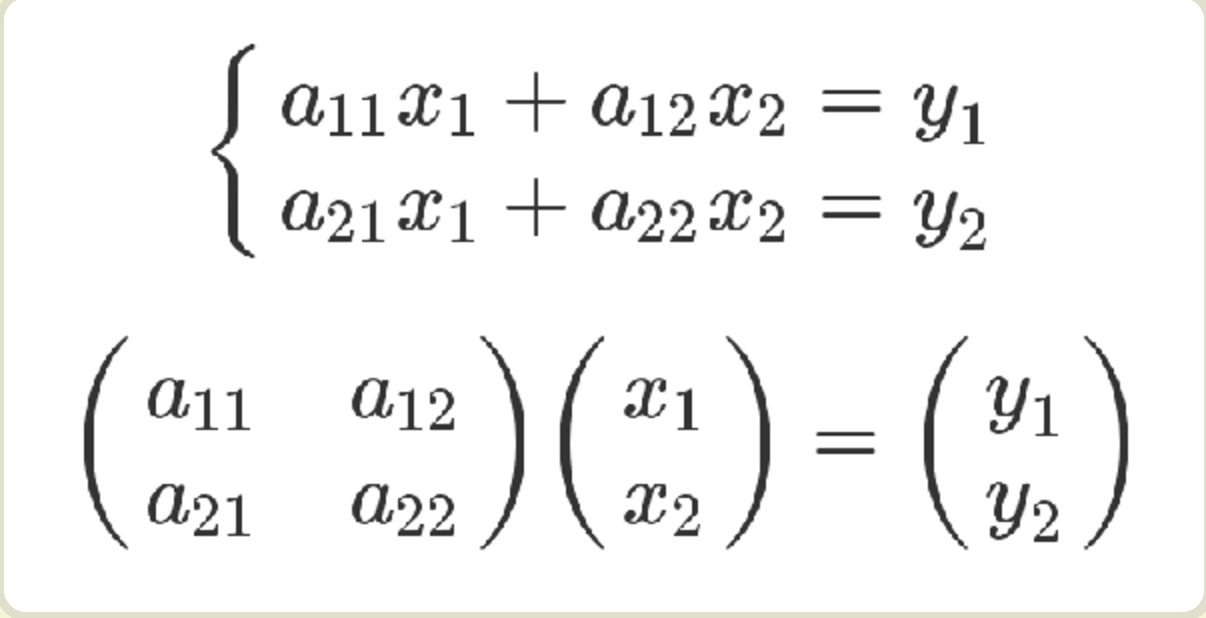
x 和 t 的关系如下。

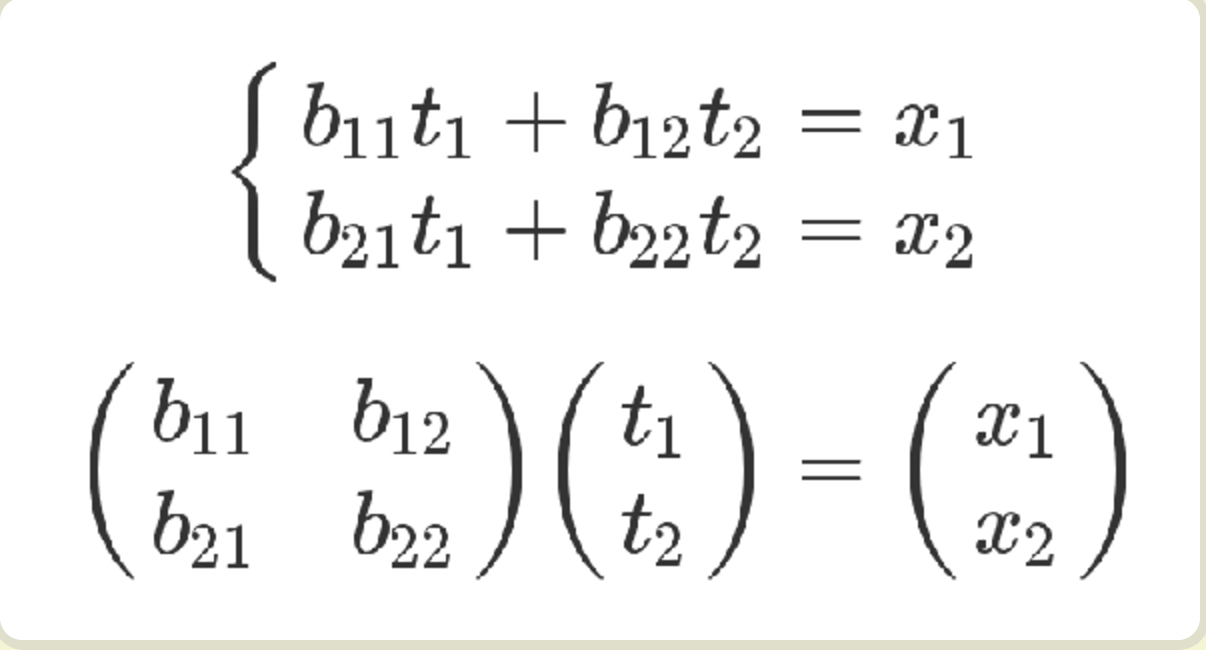
有了这两组方程式，就可以求 y 和 t 的关系。从矩阵来看，很显然，只要把第二个矩阵代入第一个矩阵即可。

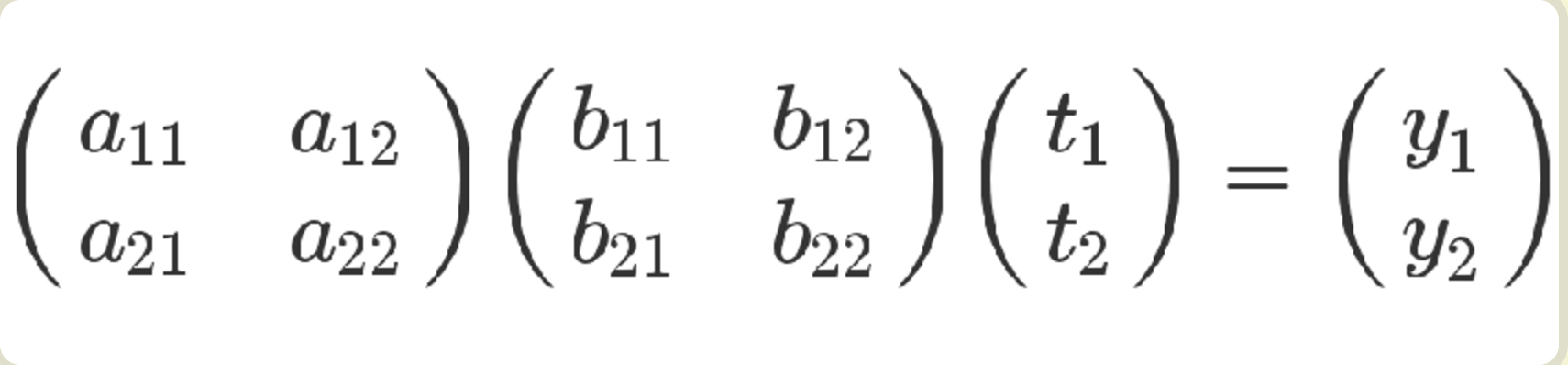
从方程式来看，也可以把第二个方程组代入第一个方程组。

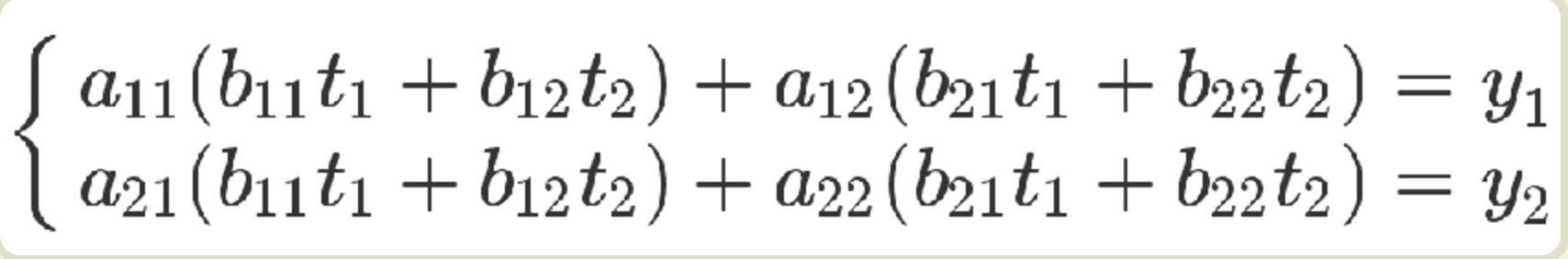
上面的方程组可以整理成下面的形式。

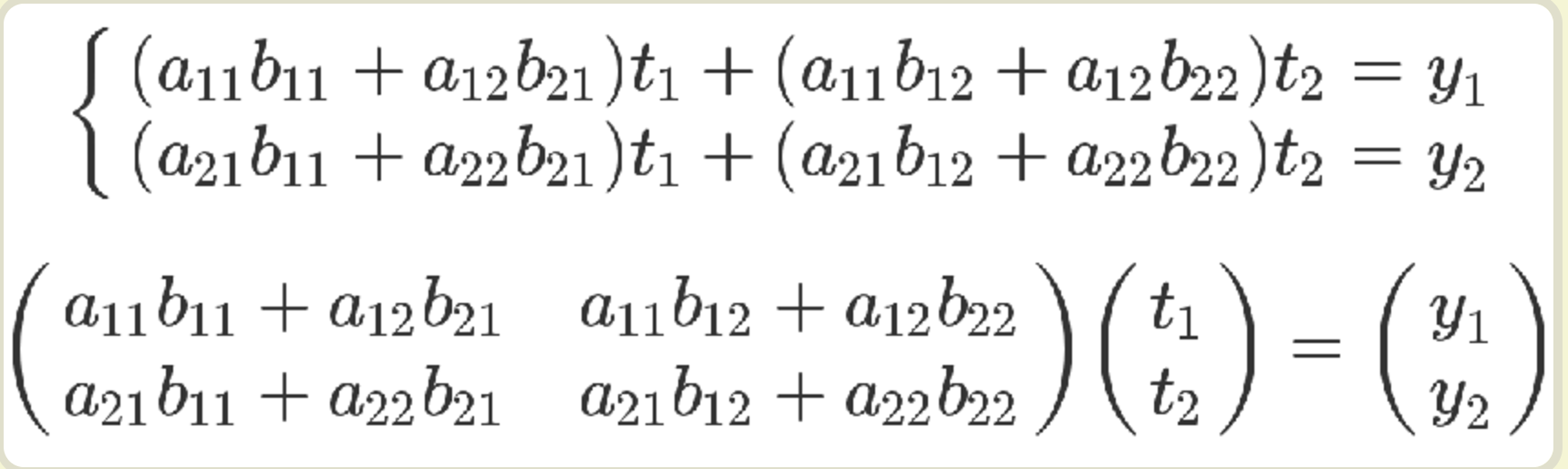
最后那个矩阵等式，与前面的矩阵等式一对照，就会得到下面的关系。

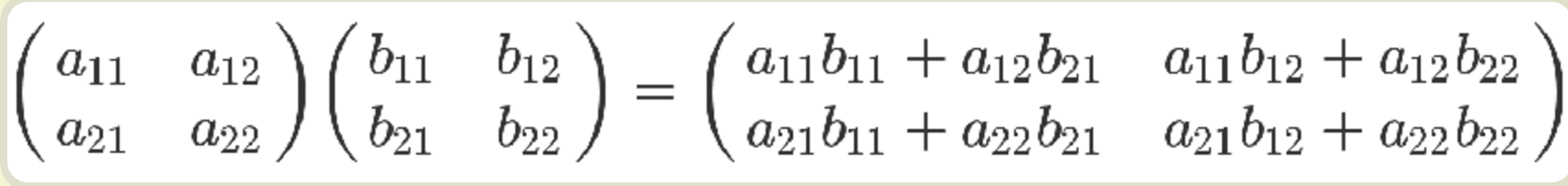
转移矩阵

题意:F(n) = F(n-1) + 2F(n-2) + n^4，且F(1) = a , F(2) = b，求F(n)%2147493647，其中a、b、n是待输入的参数

我们把解决这类题目的过程分解为如下步骤：

  1. 把非线性递推式转化为线性递推式（线性递推式可忽略第一步）
  2. 根据线性递推式得到F(n)和F(n+1)的矩阵序列
  3. 根据F(n)和F(n+1)的矩阵序列得到中间的转移矩阵
  4. 根据转移矩阵编写代码

分步拆解问题

首先把非线性递推式转换为线性递推式

二项式展开公式:

(a+b)^n=a^n+C(n,1)a^(n-1)b+C(n,2)a^(n-2)b^2+...+C(n,n-1)ab^(n-1)+b^n.

(n+1)^4 = n^4 + 4n^3 + 6n^2 + 4n + n^0

F(n+1) = F(n) + 2F(n-1) + (n+1)^4

F(n+1) = F(n) + 2F(n-1) + n^4 + 4n^3 + 6n^2 + 4n + n^0

然后我们看下面的状态转移矩阵,

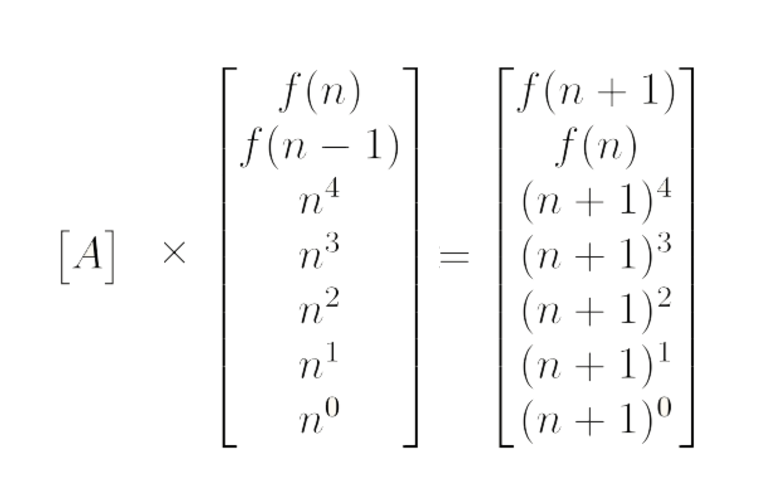
图(1)左边的矩阵表示F(n)项的矩阵，右边的矩阵表示F(n+1)项的矩阵。而中间的A矩阵就是需要求的转移矩阵。图(1)左边的矩阵怎么得到？我们看刚才得到的递归式

F(n+1) = F(n) + 2F(n-1) + n^4 + 4n^3 + 6n^2 + 4n + n^0

我们把F(n)放在矩阵顶部，表示第n项的值，然后剩下的元素F(n-1)、 n^4、n^3、n^2、n、 n^0 ，去掉系数后与F(n)一起构成一个矩阵。同理，F(n+1)的矩阵也是F(n+1)在顶部，表示第n+1项的值，然后剩下的元素F(n)、 (n+1)4、(n+1)3、(n+1)2、(n+1)、 (n+1)0 去掉系数后与F(n+1)构成一个矩阵。

好，我们现在得到了F(n)和F(n+1)的矩阵，那怎么求转移过去的矩阵A呢？首先，A是一个7×7的矩阵，且根据矩阵相乘规则，可以得到矩阵A，如下图

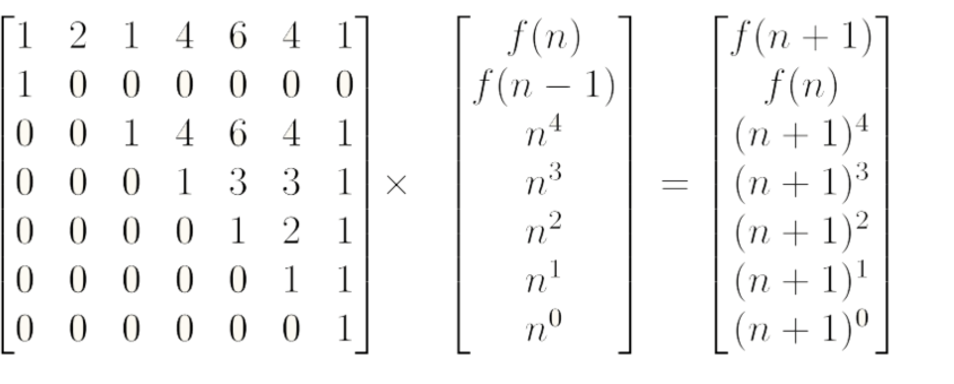
好了，到现在为止，得到了图(2)的转移矩阵后，我们解决了前三步，还剩最后一步。怎么把这个转移矩阵应用到代码里面呢？

为了表述方便。图(3)乘号左边的我们称为转移矩阵A，乘号右边的四个矩阵分别为B2、B3、B4、B5……

且我们可以得到的信息有

B2 × A = B3、 B3 × A = B4、 B4 × A = B5 ……

B2 × A^2 = B4、 B2 × A^3 = B5、 B2 × A^4 = B6 ……

然后我们惊奇的发现：B2 × A^n-2 = Bn（fn）

举例

题目大意：给出n和k，表示一个序列A[i]，求前n项A[i]的和，结果可以% 1e9+7。

A[i] = i^k * F[i]，F[i] = F[i-1] + F[i-2]（斐波那契数列）。

解题思路：

首先（i+1）^k = C(k,k) * i ^ k + C(k, k-1) * i ^ (k-1) ……… + C(k, 0) * i ^ 0.

那么定义u（n+1，k) = (n+1) ^ k * F(n+1), v(n+1, k) = (n+1) ^ k * F(n).

u(n+1, k) = (n+1)^k * F(n+1) = (n+1)^k * F(n) + (n+1)^k * F(n-1)

= ∑[1,k] C(k, i) * n^i * F(n) + ∑[1,k] C(k,i) * n^i * F(n-1) = ∑[1,k] C(k,i) * u(n, i) + ∑[1,k] C(k,i) * v(n, i);

v(n+1, k) = (n+1)^k * F(n) = ∑[1,k] C(k, i) * n^i * F(n) = ∑[1,k] C(k, i) * u(n, i);

s[n] = s[n-1] + u(n, k);

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
int len;
LL n,k;
LL c[45][45];
struct matrix{
    LL m[100][100];
}mc;
matrix multi(matrix a,matrix b){ //矩阵乘法
    matrix ans;
    for(int i=0;i<len;i++){
        for(int j=0;j<len;j++){
            ans.m[i][j]=0;
            for(int k=0;k<len;k++){
                ans.m[i][j]=(ans.m[i][j]+a.m[i][k]*b.m[k][j]%mod)%mod;
            }
        }
    }
    return ans;
}
matrix quick(matrix a, LL n){//矩阵a^n
    matrix ans,t=a;
    for(int i=0;i<=40;i++)
        ans.m[i][i]=1;
    while(n>0){
        if(n&1) ans=multi(ans,t);//矩阵相乘
        t=multi(t,t);
        n>>=1;
    }
    return ans;
}
int main()
{
    c[0][0]=1;
    c[1][0]=c[1][1]=1;
    for(int i=2;i<=40;i++){   //构造组合数c   k最大为40
        for(int j=0;j<=i;j++){
            if(j==0 || j==i) c[i][j]=1;
            else  c[i][j]=c[i-1][j-1]+c[i-1][j];
        }
    }
    while(cin>>n>>k){
        memset(mc.m,0,sizeof(mc.m));  //构造矩阵
        len=2*k+3;//最后矩阵的总列数
        mc.m[0][0]=1;
        for(int j=0;j<=k;j++){  //第一行
            mc.m[0][j+1]=c[k][j];
            mc.m[0][j+k+2]=c[k][j];
        }
        mc.m[1][1]=mc.m[1][k+2]=1; //第2到k+1行
        for(int i=1;i<=k;i++){
            for(int j=0;j<=i;j++){
                mc.m[i+1][j+1]=c[i][j];
                mc.m[i+1][j+k+2]=c[i][j];
            }
        }
        mc.m[k+2][1]=1;
        for(int i=1;i<=k;i++){
            for(int j=0;j<=i;j++){
                mc.m[i+k+2][j+1]=c[i][j];
            }
        }
        mc=quick(mc,n-1);
        LL ans=0;
        for(int i=0;i<len;i++){//求和
            ans=(ans+mc.m[0][i]%mod)%mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

转载:http://www.jianshu.com/p/25eba927d9da