欧拉函数
欧拉函数用希腊字母φ表示,φ(N)表示N的欧拉函数.
对φ(N)的值,我们可以通俗地理解为小于N且与N互质的数的个数(包含1).
欧拉函数的一些性质:
-
对于素数p, φ(p)=p-1,对于对两个素数p,q φ(pq)=pq-1
-
对于一个正整数N的素数幂分解
N=P1^q1*P2^q2*...*Pn^qn.
φ(N)=N*(1-1/P1)*(1-1/P2)*...*(1-1/Pn).
-
除了N=2,φ(N)都是偶数.
-
设N为正整数,∑φ(d)=N (d|N).
根据性质2,我们可以在O(sqrt(n))的时间内求出一个数的欧拉函数值.
1
2
3
4
5
6
7
8
9
10
11
12
|
//直接求解欧拉函数
int euler(int n){ //返回euler(n)
int res=n,a=n;
for(int i=2;i*i<=a;i++){
if(a%i==0){
res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出
while(a%i==0) a/=i;//将i的幂除尽
}
}
if(a>1) res=res/a*(a-1);
return res;
}
|
素数筛法
一个合数总是可以分解成若干个质数的乘积,那么如果把质数(最初只知道2是质数)的倍数都去掉,那么剩下的就是质数了。
(1)先把1删除(1既不是质数也不是合数)
(2)读取队列中当前最小的数2,然后把2的倍数删去
(3)读取队列中当前最小的数3,然后把3的倍数删去
(4)读取队列中当前最小的数5,然后把5的倍数删去
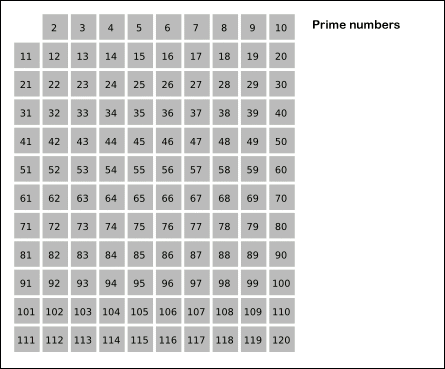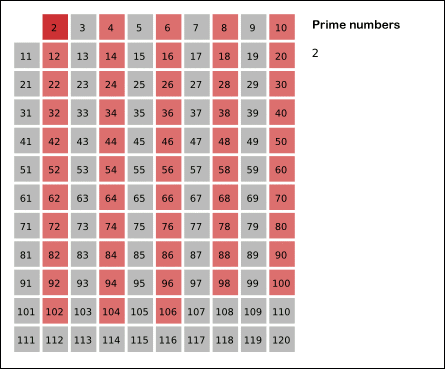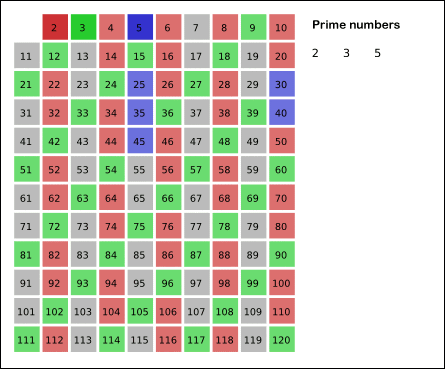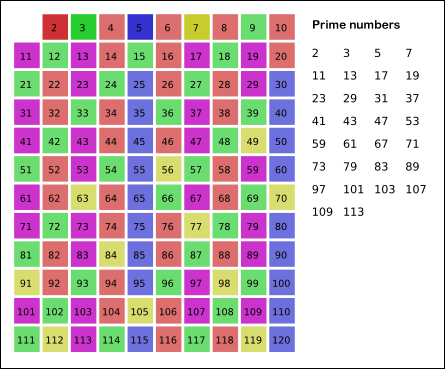
…….
(n)读取队列中当前最小的状态为true的数n,然后把n的倍数删去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
//埃拉托斯特尼尼素数筛法
int countPrimes(int n) {
if (n<=2) return 0;//2以下没有
vector<bool> num(n - 1, true);//假定全为质数
num[0] = false;
int res = 0, limit = sqrt(n);
for (int i = 2; i <= limit; ++i) {//从2到limit枚举
if (num[i - 1]) {//如果该数还没被判断非质数
for (int j = i * i; j < n; j += i) {//以该质数为因子的所有合数都被筛出来
num[j - 1] = false;
}
}
}
for (int j = 0; j < n - 1; ++j) {//求得小于n的质数的个数
if (num[j]) ++res;
}
return res;
}
|