现代编程语言,大都在标准库中包含了随机库。例如,C++ 在 C++11 标准中添加了 random 头文件,提供了现代的随机库;Python 则有 random。C++11 的随机库将生成随机数的过程在逻辑上切分成了两个步骤:随机数生成引擎和分布。在学习 C++11 的 random 库时,std::mt19937 这一随机数生成引擎的名字看起来十分奇怪,成功吸引了我的注意力。
查询后得知,std::mt19937 中的 MT 是 Mersenne Twister 的缩写,这是伪随机数生成算法的名字(梅森旋转算法);而 19937 则取自算法中用到的梅森素数 $2^{19937−1}$。这里,梅森素数是算法生成伪随机数的循环长度(period),而旋转则说的是算法内部对定长二进制串循环位移的过程。
此篇讲解梅森旋转算法的一些原理,并介绍对其的一个「爆破」方法。
伪随机数发生器质量的度量——𝑘-维 𝑣-比特准确度

基本概念
旋转

线性反馈移位寄存器、旋转之名、周期

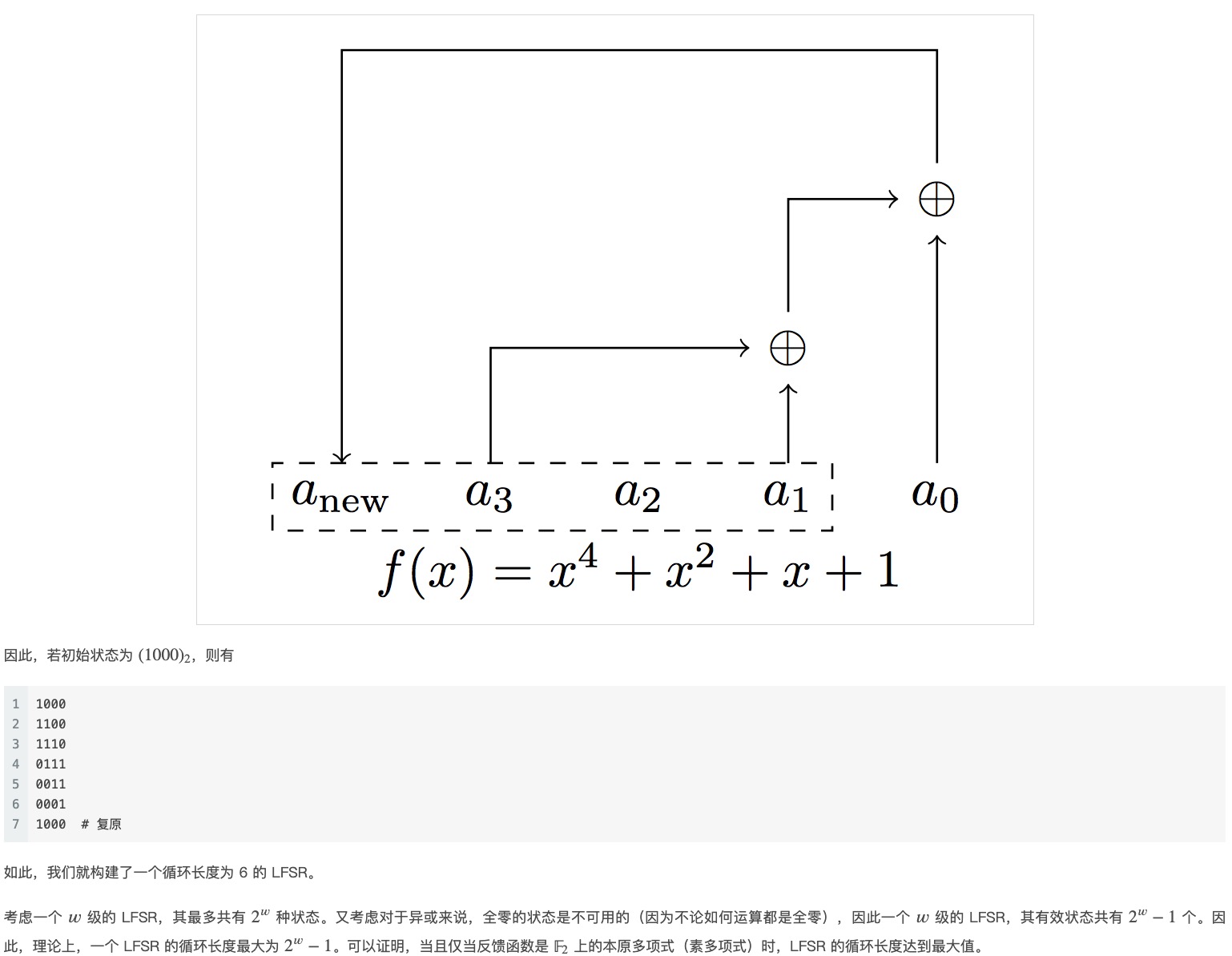
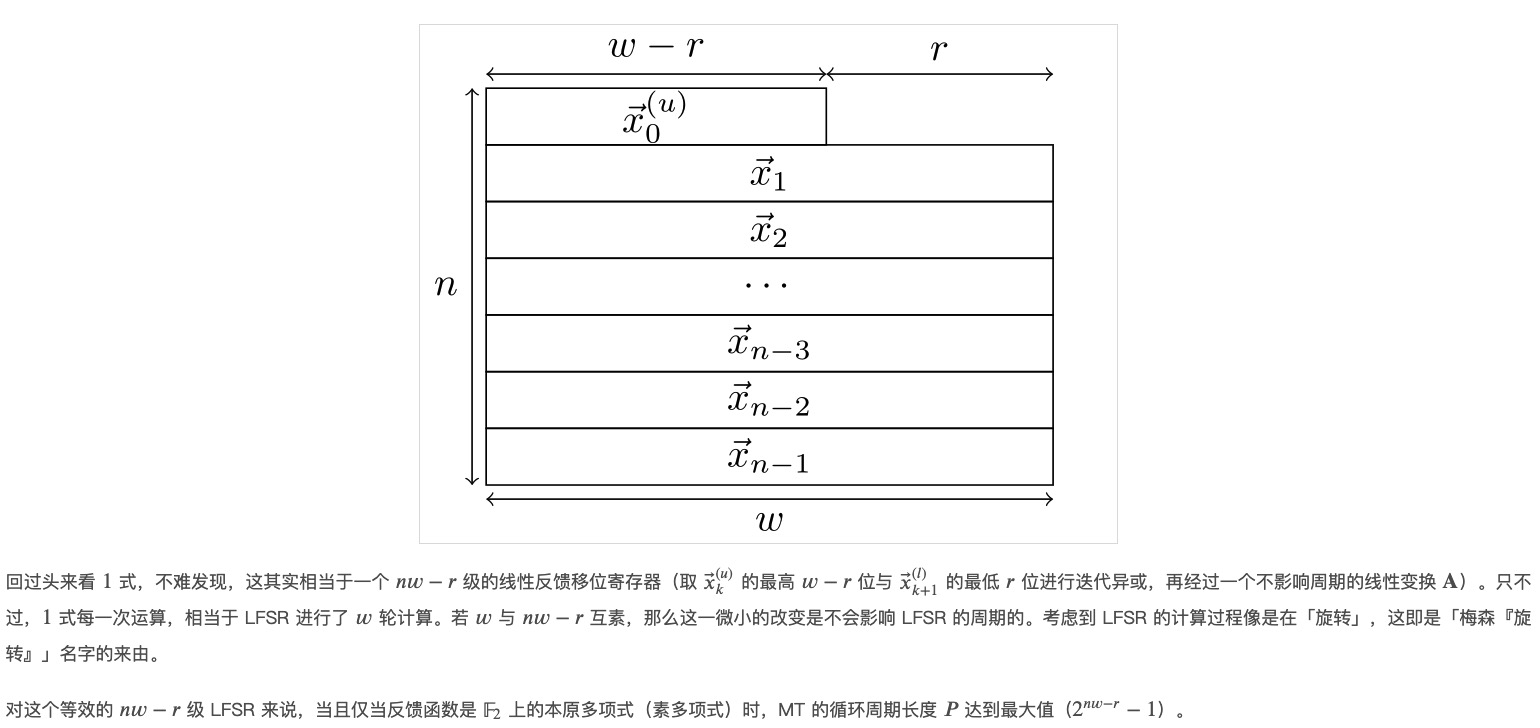
提取(tempering)输出

算法描述

再探梅森旋转

关于周期
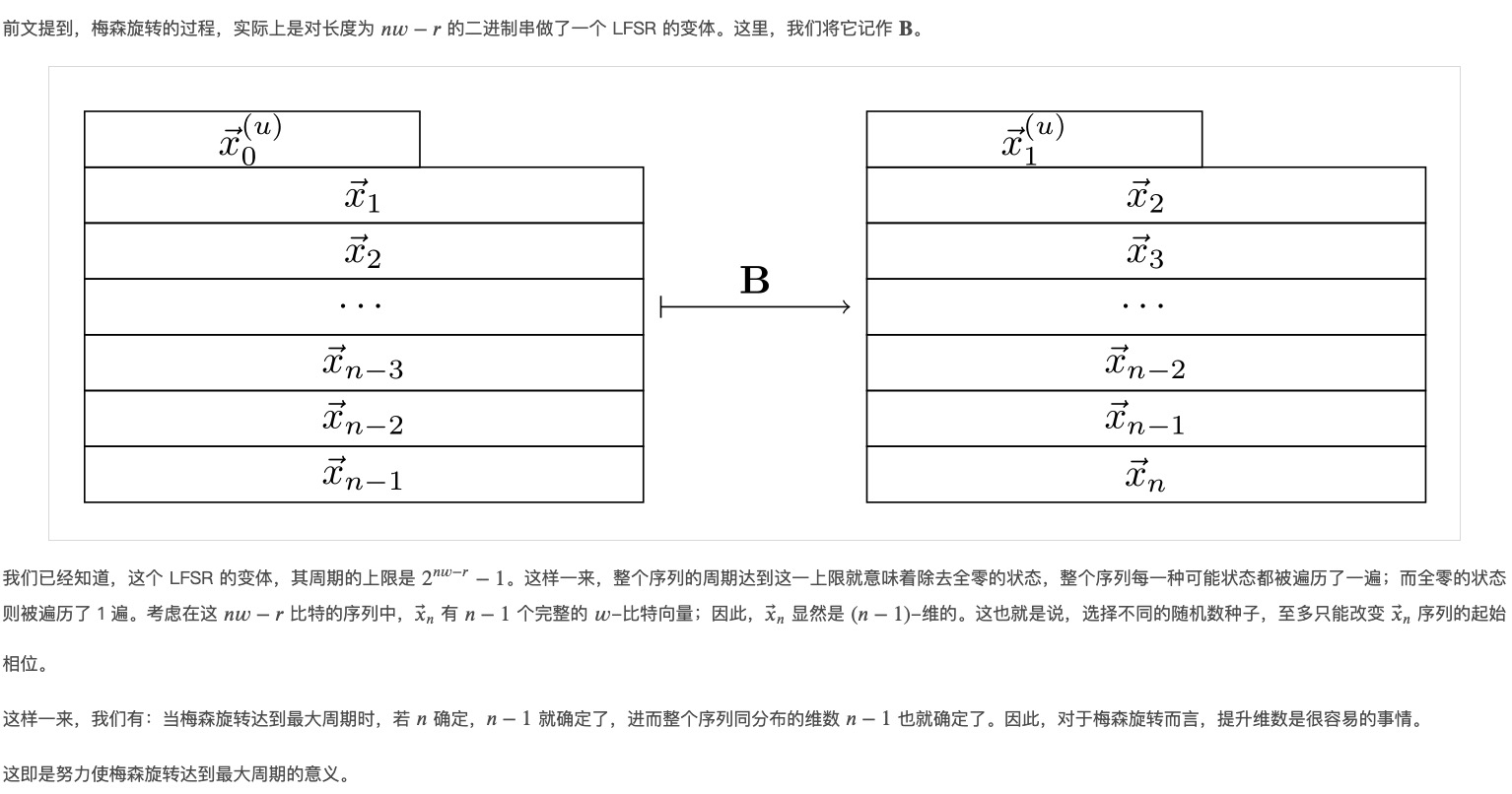
多项式素检测与参数调优

梅森旋转算法的 Python 实现
此处给出一个 Python 实现的梅森旋转算法(mt19937),为后续对算法的「爆破」提供素材。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
#! coding: utf-8
class MersenneTwister:
__n = 624
__m = 397
__a = 0x9908b0df
__b = 0x9d2c5680
__c = 0xefc60000
__kInitOperand = 0x6c078965
__kMaxBits = 0xffffffff
__kUpperBits = 0x80000000
__kLowerBits = 0x7fffffff
def __init__(self, seed = 0):
self.__register = [0] * self.__n
self.__state = 0
self.__register[0] = seed
for i in range(1, self.__n):
prev = self.__register[i - 1]
temp = self.__kInitOperand * (prev ^ (prev >> 30)) + i
self.__register[i] = temp & self.__kMaxBits
def __twister(self):
for i in range(self.__n):
y = (self.__register[i] & self.__kUpperBits) + \
(self.__register[(i + 1) % self.__n] & self.__kLowerBits)
self.__register[i] = self.__register[(i + self.__m) % self.__n] ^ (y >> 1)
if y % 2:
self.__register[i] ^= self.__a
return None
def __temper(self):
if self.__state == 0:
self.__twister()
y = self.__register[self.__state]
y = y ^ (y >> 11)
y = y ^ (y << 7) & self.__b
y = y ^ (y << 15) & self.__c
y = y ^ (y >> 18)
self.__state = (self.__state + 1) % self.__n
return y
def __call__(self):
return self.__temper()
def load_register(self, register):
self.__state = 0
self.__register = register
if __name__ == "__main__":
mt = MersenneTwister(0)
tank = set()
kLen = 100
for i in range(kLen):
t = mt()
tank.add(t)
print(t)
print(len(tank) == kLen)
|
爆破梅森旋转算法
梅森旋转算法的设计目的是优秀的伪随机数发生算法,而不是产生密码学上安全的随机数。从梅森旋转算法的结构上说,其提取算法 __temper 完全基于二进制的按位异或;而二进制按位异或是可逆的,故而 __temper 是可逆的。这就意味着,攻击者可以从梅森旋转算法的输出,逆推出产生该输出的内部寄存器状态 __register[__state]。若攻击者能够获得连续的至少 __n 个寄存器状态,那么攻击者就能预测出接下来的随机数序列。
现在我们遵循这个思路,爆破梅森旋转算法。
逆向 __temper
我们以向右移位后异或为例,首先观察原函数。
1
2
3
4
|
def right_shift_xor(value, shift):
result = value
result ^= (result >> shift)
return result
|
简单起见,我们观察一个 8 位二进制数,右移 3 位后异或的过程。
1
2
3
|
value: 1101 0010
shifted: 0001 1010 # 010 (>> 3)
result: 1100 1000
|
首先,观察到 result 的最高 shift 位与 value 的最高 shift 位是一样的。因此,在 result 的基础上,我们可以将其与一个二进制遮罩取与,得到 value 的最高 shift 位。这个遮罩应该是:1111 1111 « (8 - 3) = 1110 0000。于是我们得到 1100 0000。
其次,注意到对于异或运算有如下事实:a ^ b ^ b = a。依靠二进制遮罩,我们已经获得了 value 的最高 shift 位。因此,我们也就能得到 shifted 的最高 2 * shift 位。它应该是 1100 0000 » 3 = 0001 1000。将其与 result 取异或,则能得到 value 的最高 2 * shift 位。于是我们得到 1101 0000。
如此往复,即可复原 value。据此有代码
1
2
3
4
5
6
7
8
9
|
def inverse_right_shift_xor(value, shift):
i, result = 0, 0
while i * shift < 32:
part_mask = ((0xffffffff << (32 - shift)) & 0xffffffff) >> (i * shift)
part = value & part_mask
value ^= part >> shift
result |= part
i += 1
return result
|
对左移后取异或,也有类似分析。于是,得到对 __temper 的完整求逆代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class TemperInverser:
__b = 0x9d2c5680
__c = 0xefc60000
__kMaxBits = 0xffffffff
def __inverse_right_shift_xor(self, value, shift):
i, result = 0, 0
while i * shift < 32:
part_mask = ((self.__kMaxBits << (32 - shift)) & self.__kMaxBits) >> (i * shift)
part = value & part_mask
value ^= part >> shift
result |= part
i += 1
return result
def __inverse_left_shift_xor(self, value, shift, mask):
i, result = 0, 0
while i * shift < 32:
part_mask = (self.__kMaxBits >> (32 - shift)) << (i * shift)
part = value & part_mask
value ^= (part << shift) & mask
result |= part
i += 1
return result
def __inverse_temper(self, tempered):
value = tempered
value = self.__inverse_right_shift_xor(value, 18)
value = self.__inverse_left_shift_xor(value, 15, self.__c)
value = self.__inverse_left_shift_xor(value, 7, self.__b)
value = self.__inverse_right_shift_xor(value, 11)
return value
def __call__(self, tempered):
return self.__inverse_temper(tempered)
|
爆破
逆向 __temper() 之后,只要获得足够的状态,即可构建出梅森旋转内部的寄存器状态。因此有如下验证代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class MersenneTwisterCracker:
__n = 624
def __init__(self, mt_obj):
inverser = TemperInverser()
register = [inverser(mt_obj()) for i in range(self.__n)]
self.__mt = MersenneTwister(0)
self.__mt.load_register(register)
def __call__(self):
return self.__mt()
if __name__ == "__main__":
mt = MersenneTwister(0)
for i in range(100):
mt()
mtc = MersenneTwisterCracker(mt)
for i in range(100):
assert(mt() == mtc())
|
运行后,Python 没有抛出异常,顺利推出。这说明 mtc 已能够成功预测 mt 之后的任意顺序输出。
总结
梅森旋转算法,是一个优秀的伪随机数发生算法。在伪随机数的评价体系中,它是一个相当优秀的算法:周期长、均匀性好、速度快(基本都是位运算)。在条件允可的情形下,若有使用随机数的需求,应首先考虑梅森旋转算法。
同时也应该注意到,梅森旋转算法不是为了密码学随机而设计的——在获得足够连续输出的情况下,梅森旋转算法接下来的输出值是可以准确预测的。梅森旋转算法容易被爆破的根源在于,其提取输出函数是可逆的,因此暴露了其内部状态。若要产生密码学上的随机数,可考虑在梅森旋转算法之后,拼接一值得信赖的单向杂凑函数(如 sha256)。否则,若直接用梅森旋转算法的输出值作密码学用途,则有信息泄露的风险,应引起注意。
错误应用梅森旋转算法,导致高危漏洞的一个典型是 Discuz! 的密码重置漏洞。
转载:https://liam.page/2018/01/12/Mersenne-twister/









