BFS

4. 举例

题目:

用一个整型矩阵matrix表示一个网络，1代表有路，0代表无路，每一个位置只要不越界，都有上下左右4个方向，求从最左上角到最右下角的最短通路值。

例如，matrix为:

通路只有一条，由12个1构成，所以返回12。

解析:

使用宽度优先遍历即可，时间复杂度为O(N*M).具体过程如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


	public static int minPathValue(int[][] m) {
		if (m == null || m.length == 0 || m[0].length == 0 || m[0][0] != 1
				|| m[m.length - 1][m[0].length - 1] != 1) {
			return 0;
		}
		int res = 0;
		int[][] map = new int[m.length][m[0].length];
		map[0][0] = 1;
		Queue<Integer> rQ = new LinkedList<Integer>();
		Queue<Integer> cQ = new LinkedList<Integer>();
		rQ.add(0);
		cQ.add(0);
		int r = 0;
		int c = 0;
		while (!rQ.isEmpty()) {
			r = rQ.poll();
			c = cQ.poll();
			if (r == m.length - 1 && c == m[0].length - 1) {
				return map[r][c];
			}
			walkTo(map[r][c], r - 1, c, m, map, rQ, cQ); // up
			walkTo(map[r][c], r + 1, c, m, map, rQ, cQ); // down
			walkTo(map[r][c], r, c - 1, m, map, rQ, cQ); // left
			walkTo(map[r][c], r, c + 1, m, map, rQ, cQ); // right
		}
		return res;
	}

Dijkstra

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2.算法描述

1)算法思想：

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，

第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），

第二组为其余未确定最短路径的顶点集合（用U表示），

按最短路径长度的递增次序依次把第二组的顶点加入S中。

在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。

此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。
从U中选取一个距离v最小的顶点k，把k加入S中（该选定的距离就是v到k的最短路径长度）。
以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。
重复步骤2和3直到所有顶点都包含在S中。

执行动画过程如下图

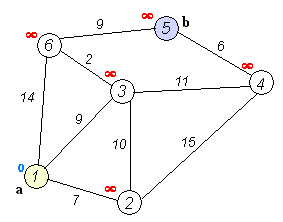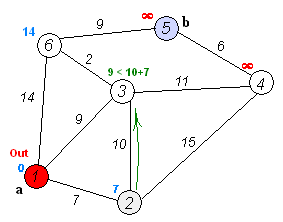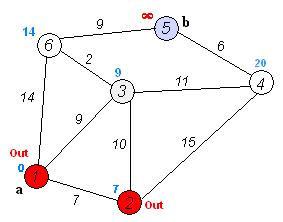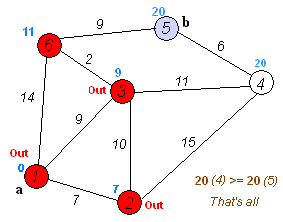
4.举例

题目大意：有N个点，给出从a点到b点的距离，当然a和b是互相可以抵达的，问从1到n的最短距离.

解题思路：这题要注意的是有重边，dijkstra的算法需要考虑下，bellman-ford和spfa可以忽略这个问题.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75


#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=1005;
const int M=2005;
const int inf=(1<<29);
int n,m;
int d[N];
struct
{
	int v,w,next;
}edge[2*M];
int edgehead[N];
//head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.
int k;
bool vis[N];
void addedge(int u,int v,int w)
{
	edge[k].next=edgehead[u];//表示与第k条边同起点的上一条边的存储位置（头插法）
	edge[k].w=w;            //边权值
	edge[k].v=v;         //表示第k条边的终点
	edgehead[u]=k++;
}
//链式前向星也是一种通过存储边的信息的方式存储图的数据结构，可以静态建立邻接表。它将边存放在数组中，
//把数组中的边按照起点顺序排序，前向星就构造完成了。为了查询方便，经常会有一个数组存储起点为Vi的第一条边的位置。
struct cmp
{
	bool operator ()(const int a,const int b)
	{
		return d[a]>d[b];
	}
};
int dijstra(int s)
{
	priority_queue<int,vector<int>,cmp> que;
	for(int i=1;i<=n;i++)//预处理每个点到源点的距离
		d[i]=inf;
	d[s]=0;
	memset(vis,0,sizeof(vis));
	que.push(1);
	while(!que.empty())
	{
		int u=que.top();
		que.pop();
		if(vis[u])//排除已加入到最短路的顶点
			continue;
		vis[u]=true;
		for(int i=edgehead[u];i;i=edge[i].next)//枚举所有邻接边
		{
			int v=edge[i].v;
			int w=edge[i].w;
			if(!vis[v]&&d[v]>d[u]+w)
			{
				d[v]=d[u]+w;
				que.push(v);
			}
		}
	}
	return d[n];
}
int main()
{
	scanf("%d%d",&m,&n);
	int u,v,w;
	k=1;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&u,&v,&w);
		addedge(u,v,w);
		addedge(v,u,w);
	}
	printf("%d\n",dijstra(1));
	return 0;
}

Bellman_Ford

1.定义概览

单源最短路径：给定一个图,和一个源顶点src,找到从src到其它所有所有顶点的最短路径，图中可能含有负权值的边。

关于这个问题我们已经讨论了迪杰斯特拉算法。

Dijksra的算法是一个贪婪算法,时间复杂度是O(VLogV)(使用最小堆)。但是迪杰斯特拉算法在有负权值边的图中不适用,

Bellman-Ford适合这样的图。在网络路由中，该算法会被用作距离向量路由算法。

Bellman-Ford也比迪杰斯特拉算法更简单和同时也适用于分布式系统。但Bellman-Ford的时间复杂度是O(VE),E为边的个数，这要比迪杰斯特拉算法慢。

2. 算法描述

给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为, Distant[s]为0；

以下操作循环执行至多n-1次，n为顶点数：

对于每一条边e(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则令Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；

若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；为了检测图中是否存在负环路，即权值之和小于0的环路。

对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) < Distant[v]的边，则图中存在负环路，即是说该图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。

可知，Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).

3. 算法步骤：

初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
```
 d（v） > d (u) + w(u,v)
```
则返回false，表示途中存在从源点可达的权为负的回路。

之所以需要第三部分的原因，是因为，如果存在从源点可达的权为负的回路。则应为无法收敛而导致不能求出最短路径。

4. 举例

给定N种货币，某些货币之间可以相互兑换，现在给定一些兑换规则，问能否从某一种货币开始兑换，经过一些中间货币之后，最后兑换回这种货币，并且得到的钱比之前的多。

可以把初始兑换的货币看成源点，采用bellman-ford进行求解，若可以实现要求，则说明图中存在可以无限增大的环，这个可以通过bellman-ford算法判断环是否存在求出来，若在求解过程中发现已经兑换回原货币，并且钱比之前多，则可以直接退出算法。由于兑换过程中每种货币值必须为非负的，因此可以把所有初始路径长度设置为0，按照兑换方式对边进行松弛。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69


#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
const int MAXN=110;
const int MAXE=210;//两倍
double dist[MAXN];
int tol;//边的总数
int D[MAXE][2];//存边的起点和终点
double C[MAXE][2];//存汇率和手续费
bool Bellman(int start,int n,double V)
{
    for(int i=1;i<=n;i++) dist[i]=0;////这里与bellman的目的刚好相反。初始化为源点到各点距离无穷小
    dist[start]=V;//即bellman本用于找负环，求最小路径，本题是利用同样的思想找正环，求最大路径
    for(int i=1;i<n;i++)//做n-1次（n-1个点）
//Bellman-Ford算法不一定要循环n-1次， n为顶点个数只要在某次循环过程中，考虑每条边后，
//源点到所有顶点的最短路径长度都没有变，那么Bellman-Ford算法就可以提前结束了
    {
        bool flag=false;//优化
        for(int j=0;j<tol;j++)//枚举每条边
        {
            int u=D[j][0];
            int v=D[j][1];
            if(dist[v] < (dist[u]-C[j][1])*C[j][0])//进行比较的是"某点到自身的权值"和"某点到另一点的权值"
            {
                flag=true;//存在可用边，不能提前结束
                dist[v]=(dist[u]-C[j][1])*C[j][0];
            }
        }
        if(!flag)return false;//没有更新，循环提前结束，也表示不存在正环
    }
//做了n-1次的全部边松弛操作之后，就确定了所有点的最短路径值。
//如果做第n次全部边松弛操作的时候，还有点的最短值会被更新，则说明图里是存在正环的。
    for(int j=0;j<tol;j++)
      if(dist[D[j][1]]<(dist[D[j][0]]-C[j][1])*C[j][0])//正环能够无限松弛
        return true;//有正环
    return false;
}
int main()
{
    int n;
    int M;
    int a,b;
    double c,d,e,f;
    int S;
    double V;
    while(scanf("%d%d%d%lf",&n,&M,&S,&V)!=EOF)//存储数据
    {
        tol=0;
        while(M--)
        {
            scanf("%d%d%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f);
            D[tol][0]=a;
            D[tol][1]=b;
            C[tol][0]=c;
            C[tol][1]=d;
            tol++;
            D[tol][0]=b;
            D[tol][1]=a;
            C[tol][0]=e;
            C[tol][1]=f;
            tol++;
        }
        if(Bellman(S,n,V)) printf("YES\n");//S为源点的钱，n为源点钱的数目
        else printf("NO\n");
    }
    return 0;
}

SPFA

1. 定义概览

spfa可以看成是bellman-ford的队列优化版本，正如在前面讲到的，bellman每一轮用所有边来进行松弛操作可以多确定一个点的最短路径，但是用每次都把所有边拿来松弛太浪费了，不难发现，只有那些已经确定了最短路径的点所连出去的边才是有效的，因为新确定的点一定要先通过已知(最短路径的)节点。

所以我们只需要把已知节点连出去的边用来松弛就行了，但是问题是我们并不知道哪些点是已知节点，不过我们可以放宽一下条件，找哪些可能是已知节点的点，也就是之前松弛后更新的点，已知节点必然在这些点中。

所以spfa的做法就是把每次更新了的点放到队列中记录下来。

在实现上，bellman-ford可以用边集数组或链式前向星来实现。

而spfa则只能用链式前向星实现。

在效率上，当图很稠密的时候spfa就退化成和bellman -ford差不多了，因为对于入队的每个节点都要和很多节点去进行松弛操作。

2. 算法描述

简洁起见，我们约定有向加权图G不存在负权回路，即最短路径一定存在。我们用数组d记录每个结点的最短路径估计值，而且用邻接表来存储图G。

我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且 v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。

SPFA和经过简单优化的Bellman-Ford无论在思想上还是在复杂度上都有相似之处。算法是迭代式的，最短路径的估计值都是临时的。算法思想是不断地逼近最优解，只在最后一步才确定想要的结果。

但是他们实现的方式上存在差异。正因为如此，它们的时间复杂度其实有较大差异的。在Bellman-Ford算法中，要是某个点的最短路径估计值更新了，那么我们必须对所有边指向的终点再做一次松弛操作；在SPFA算法中，某个点的最短路径估计值更新，只有以该点为起点的边指向的终点需要再做一次松弛操作。在极端情况下，后者的效率将是前者的n倍，一般情况下，后者的效率也比前者高出不少。基于两者在思想上的相似，可以这样说，SPFA算法其实是Bellman-Ford算法的一个进一步优化的版本。

3. 算法步骤

算法大致流程是用一个队列来进行维护。初始时将源加入队列。每次从队列中取出一个元素，并对所有与他相邻的点进行松弛，若某个相邻的点松弛成功，则将其入队。直到队列为空时算法结束。

这个算法，简单的说就是队列优化的bellman-ford,利用了每个点不会更新次数太多的特点发明的此算法SPFA——Shortest Path Faster Algorithm，它可以在O(kE)的时间复杂度内求出源点到其他所有点的最短路径，可以处理负边。

SPFA的实现甚至比Dijkstra或者Bellman_Ford还要简单：

设Dist代表S到I点的当前最短距离，Fa代表S到I的当前最短路径中I点之前的一个点的编号。开始时Dist全部为+∞，只有Dist[S]=0，Fa全部为0。
维护一个队列，里面存放所有需要进行迭代的点。初始时队列中只有一个点S。用一个布尔数组记录每个点是否处在队列中。
每次迭代，取出队头的点v，依次枚举从v出发的边v->u，设边的长度为len，判断Dist[v]+len是否小于 Dist[u]，若小于则改进Dist[u]，将Fa[u]记为v，并且由于S到u的最短距离变小了，有可能u可以改进其它的点，所以若u不在队列中，就将它放入队尾。这样一直迭代下去直到队列变空，也就是S到所有的最短距离都确定下来，结束算法。
若一个点入队次数超过n，则有负权环。

SPFA 在形式上和宽度优先搜索非常类似，不同的是宽度优先搜索中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是一个点改进过其它的点之后，过了一段时间可能本身被改进，于是再次用来改进其它的点，这样反复迭代下去。设一个点用来作为迭代点对其它点进行改进的平均次数为k，有办法证明对于通常的情况，k在2左右。

4. 举例

题目大意：虫洞问题，现在有n个点，m条边，代表现在可以走的通路，比如从a到b和从b到a需要花费c时间，现在在地上出现了w个虫洞，虫洞的意义就是你从a到b话费的时间是-c(时间倒流,并且虫洞是单向的)，现在问你从某个点开始走，能回到从前.

解题思路：其实给出了坐标，这个时候就可以构成一张图，然后将回到从前理解为是否会出现负权环，用SPFA就可以解出了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
int F,N,M,W;
const int INF = 1 << 30;
struct Edge {
    int e,w;
    Edge(int ee,int ww):e(ee),w(ww) { }
};
vector<Edge> G[1000]; //整个有向图
int updateTimes[1000]; //最短路的改进次数
int dist[1000]; //dist[i]是源到i的目前最短路长度
int Spfa(int v) {
    for( int i = 1; i <= N; ++i)//初始化所有边到源的最短距离
        dist[i] = INF;
    dist[v] = 0;//源点
    queue<int> que; que.push(v);
    memset(updateTimes ,0,sizeof(updateTimes));
    while( !que.empty()) {
        int s = que.front();
        que.pop();
        for( int i = 0;i < G[s].size(); ++i) {//枚举s的所有邻边
            int e = G[s][i].e;
            if( dist[e] > dist[s] + G[s][i].w ) {
                dist[e] = dist[s] + G[s][i].w;
//由于S到e的最短距离变小了，有可能e可以改进其它的点，所以若u不在队列中，就将它放入队尾。
                que.push(e);
                ++updateTimes[e];//维护改进次数
                if( updateTimes[e] >= N) return true;//若一个点最短路被改进的次数达到n ，则有负权环
            }
        }
    }
    return false;
}
int main(){
    cin >> F;
    while( F--) {
        cin >> N >> M >> W;
        for( int i = 1; i <1000; ++i)//清空vector
            G[i].clear();
        int s,e,t;
        for( int i = 0; i < M; ++ i) {//正权边（双向）
            cin >> s >> e >> t;
            G[s].push_back(Edge(e,t));
            G[e].push_back(Edge(s,t));
        }
        for( int i = 0;i < W; ++i) {//负权边（单向）
            cin >> s >> e >> t;
            G[s].push_back(Edge(e,-t));
        }
        if( Spfa(1))
            cout << "YES" <<endl;
        else cout << "NO" <<endl;
    }
}

Floyd

1. 定义概览

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3)，空间复杂度为O(N2)。

2. 算法思想

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

3. 算法步骤

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

4. 举例

题意：众所周知，证券经纪业依靠的就是过度的传言。您需要想出股票经纪人中传播假情报的方法，让您的雇主在股票市场的占据优势。为了获得最大的效果，你必须蔓延最快的方式谣言。

不幸的是你，股票经纪人信息只信任他们的“可靠来源”，这意味着你在你传播谣言之前必须考虑到他们的接触结构。它需要特定股票经纪人和一定的时间把谣言传递给他的每一位同事。你的任务将是写一个程序，告诉您选择哪一个股票经纪人作为谣言的出发点和所花费多少时间将谣言扩散到整个社会的股票经纪人。这一期限是衡量过去的人收到信息所需的时间。输入

你的程序包含多组股票经纪人的输入数据。每组以股票经纪人的人数开始。接下来的几行是每个经纪人与其他人接触的一些信息，包括这些人都是谁，以及将讯息传达到他们所需的时间。每个经纪人与其他人接触信息的格式如下：开头的第一个数表示共有n个联系人，接下来就有n对整数。每对整数列出的第一个数字指的是一个联系人（例如，一个'1’是指编号1的人），其次是在传递一个信息给那个人时所采取分钟的时间。没有特殊的标点符号或空格规则。

每个人的编号为1至经纪人数目。所花费的传递时间是从1到10分钟（含10分种）。股票经纪的人数范围是从1到100。当输入股票经纪人的人数为0时，程序终止。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#include<stdio.h>
int stb[102][102];
int min(int x,int y){return x<y?x:y;}//求最小值
void Floyd(int n)  //用floyd算法求出所有结点对的最短路径
{
      int i,j,k;
      for(k=1;k<=n;k++)
          for(i=1;i<=n;i++)
              for(j=1;j<=n;j++)
                  stb[i][j]=min(stb[i][j],stb[i][k]+stb[k][j]);
}
int main()
{
    int i,j;
    int num,num1,n,dis;
    int line,ansmix,linemax;
    while(scanf("%d",&num)&&num)//输入，num为0结束
    {
        for(i=1;i<=num;i++)//数组初始化
            for(j=1;j<=num;j++)
                stb[i][j]=1000010;
        for(i=1;i<=num;i++)
        {
            scanf("%d",&num1);
            stb[i][i]=0;
            for(j=0;j<num1;j++)
            {
                scanf("%d %d",&n,&dis);
                stb[i][n]=dis;//输入数据
            }
        }
        Floyd(num);//找出每两个点的最短路径
        ansmix=1000010;
        for(i=1;i<=num;i++)
        {
            linemax=0;
            for(j=1;j<=num;j++)
            {
                /*找出所有最短路径最长的长度，也就是第i个人向其他人发出
                消息，所有人都收到消息的最短时间*/
                if(stb[i][j]>linemax)
                {
                    linemax=stb[i][j];
                }
            }
            if(linemax<ansmix)
            {
                ansmix=linemax;//找出最短时间
                line=i;//确定是哪个人
            }
        }
        if(ansmix==1000010)
            printf("disjoint\n");
        else
            printf("%d %d\n",line,ansmix);
    }
}

最短路径算法总结

文章目录

BFS

4. 举例

Dijkstra

1.定义概览

2.算法描述

1)算法思想：

2)算法步骤：

4.举例

Bellman_Ford

1.定义概览

2. 算法描述

3. 算法步骤：

4. 举例

SPFA

1. 定义概览

2. 算法描述

3. 算法步骤

4. 举例

Floyd

1. 定义概览

2. 算法思想

3. 算法步骤

4. 举例