Prim
基本思想
Prim算法根据点进行求解.
对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边
算法步骤
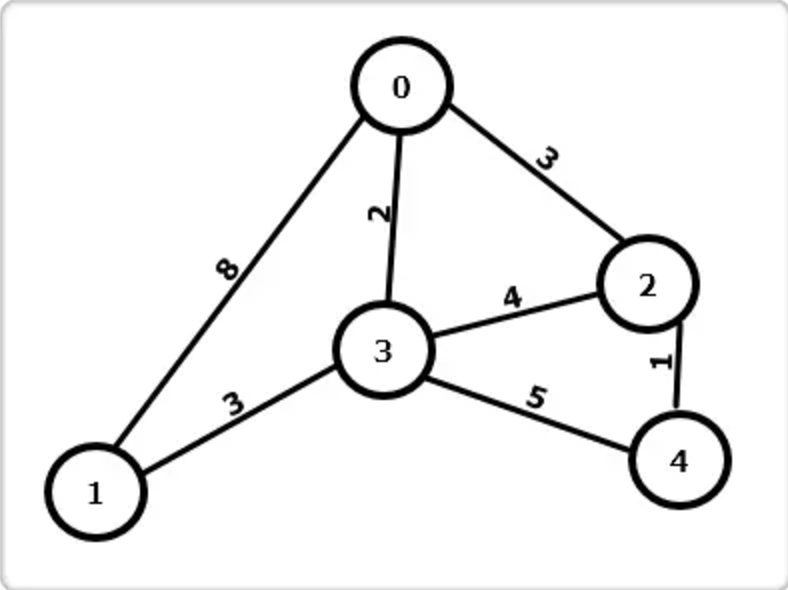
随机选一起点,假如为 0,low_cost[i]表示以 i 为终点的边的权值。其过程描述如下:
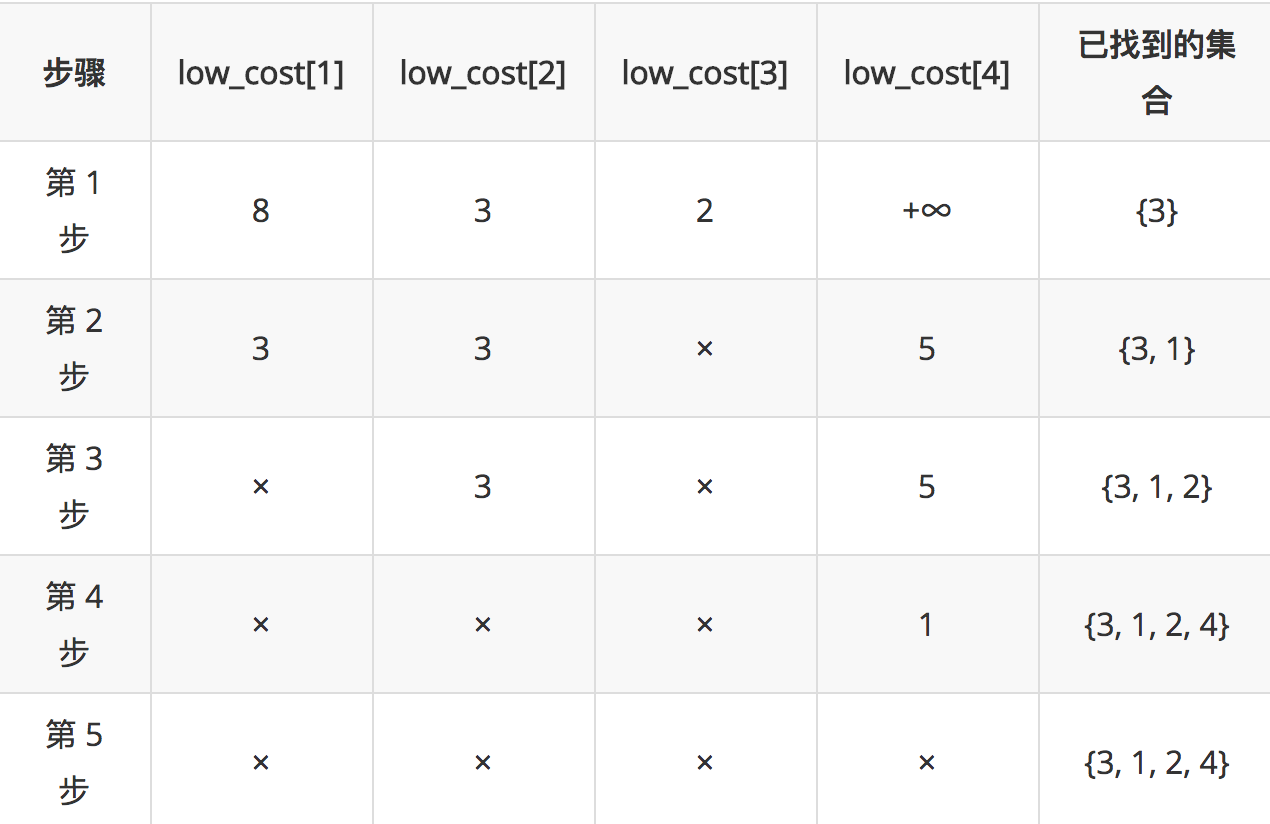
第 1 步:从起点 0 开始,找到与其邻接的点:1,2,3,更新low_cost[]数组,因 0 不与 4 邻接,故low_cost[4]为正无穷。在low_cost[]中找到最小值,其顶点为 3,即此时已找到最小生成树中的一条边:0→3。
第 2 步:从 3 开始,继续更新low_cost[]数组:3 与 1 邻接,因3→1比low_cost[1]小,故更新low_cost[1]为 3;3 与 2 邻接,因3→2比low_cost[2]大,故不更新low_cost[2] ;3 与 4 邻接,因3→4比low_cost[4]小,故更新low_cost[4]为 5。在low_cost[]中找到最小值,其顶点为 1 或者 2,随便取一个即可,我们这里取 1。即此时又找到一条边:3→1 。
第 3 步:从 1 开始,继续更新low_cost[]数组:因与 1 邻接的点都被放入最小生成树中,故不更新,直接在low_cost[]中找到最小值,其顶点为 2,即此时又找到一条边:0→2。
第 4 步:从 2 开始,继续更新low_cost[]数组:2 与 4 邻接,因2→4比low_cost[4]小,故更新low_cost[4]为 1。在low_cost[]中找到最小值,其顶点为 4,即此时又找到一条边:2→4。
第 5 步:最小生成树完成,停止。
举例
题目大意:给定一个N村庄和一个N^2的邻接矩阵表示每两个村庄间的距离,求将这N个点联通所需的最小电线长度.
思路:典型的最小生成树,我用的prim算法,就是开始随便取一个点,找出这个点和为加入的哪个点距离最短,再将那个点也加入到被选中的集合中,反复重复这个过程直到将所有点加入到被选中集合。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
const int INFINITE = 1 << 30;
struct Edge
{
int v; //边端点,另一端点已知(是已求得最小生成树的某一点,不需要具体知道是哪一个顶点)
int w; //边权值,也用来表示v到在建最小生成树的距离
Edge(int v_ = 0, int w_ = INFINITE):v(v_),w(w_) { }//构造函数
bool operator <(const Edge & e) const
{
return w > e.w; //在队列里,边权值越小越优先
}
};
vector< vector <Edge> > G(110); //图的邻接表
int HeapPrim(const vector<vector<Edge> > & G, int n)
//G是邻接表,n是顶点数目,返回值是最小生成树权值和
{
int i,j,k;
Edge xDist(0,0);
priority_queue<Edge> pq; //存放顶点及其到在建生成树的距离
vector<int> vDist(n); //各顶点到已经建好的那部分树的距离
vector<int> vUsed(n);//标记顶点是否已经被加入最小生成树
int nDoneNum = 0; //已经被加入最小生成树的顶点数目
for( i = 0;i < n;i ++ ) {//初始化所有顶点
vUsed[i] = 0;
vDist[i] = INFINITE;
}
nDoneNum = 0;
int nTotalW = 0; //最小生成树总权值
pq.push(Edge(0,0)); //开始只有顶点0,它到最小生成树距离0
while( nDoneNum < n && !pq.empty() ) {
do {//每次从队列里面拿离在建生成树最近的点
xDist = pq.top(); pq.pop();
} while( vUsed[xDist.v] == 1 && ! pq.empty());//排除已经进入MST的边
if( vUsed[xDist.v] == 0 ) {//当前边未进入MST
nTotalW += xDist.w; vUsed[xDist.v] = 1; nDoneNum ++;//维护相关值
for( i = 0;i < G[xDist.v].size();i ++ ) {//更新新加入点的邻点,放入队列中
int k = G[xDist.v][i].v;
if( vUsed[k] == 0) {//如果该点未被放入MST
int w = G[xDist.v][i].w ;
if( vDist[k] > w ) {//维护该点到树的距离
vDist[k] = w;
pq.push(Edge(k,w));
}
}
}
}
}
if( nDoneNum < n )
return -1; //图不连通
return nTotalW;
}
//考察了所有的边,且考察一条边时 可能执行 pq.push(Edge(k,w)) 故复杂度O(ELogV)
int main()
{
int N;
while(cin >> N) {
for( int i = 0;i < N; ++i)
G[i].clear();
for( int i = 0; i < N; ++i)
for( int j = 0; j < N; ++j) {//邻接表存放图
int w;
cin >> w;
G[i].push_back(Edge(j,w));
}
cout << HeapPrim(G,N) << endl;
}
}
|
Kruskal
基本思想
Kruskal根据边进行求解.
Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。
算法步骤
(1)将图G看做一个森林,每个顶点为一棵独立的树
(2)将所有的边加入集合S,即一开始S = E
(3)从S中拿出一条最短的边(u,v),如果(u,v)不在同一棵树内,则连接u,v合并这两棵树,同时将(u,v)加入生成树的边集E'
(4)重复(3)直到所有点属于同一棵树,边集E’就是一棵最小生成树
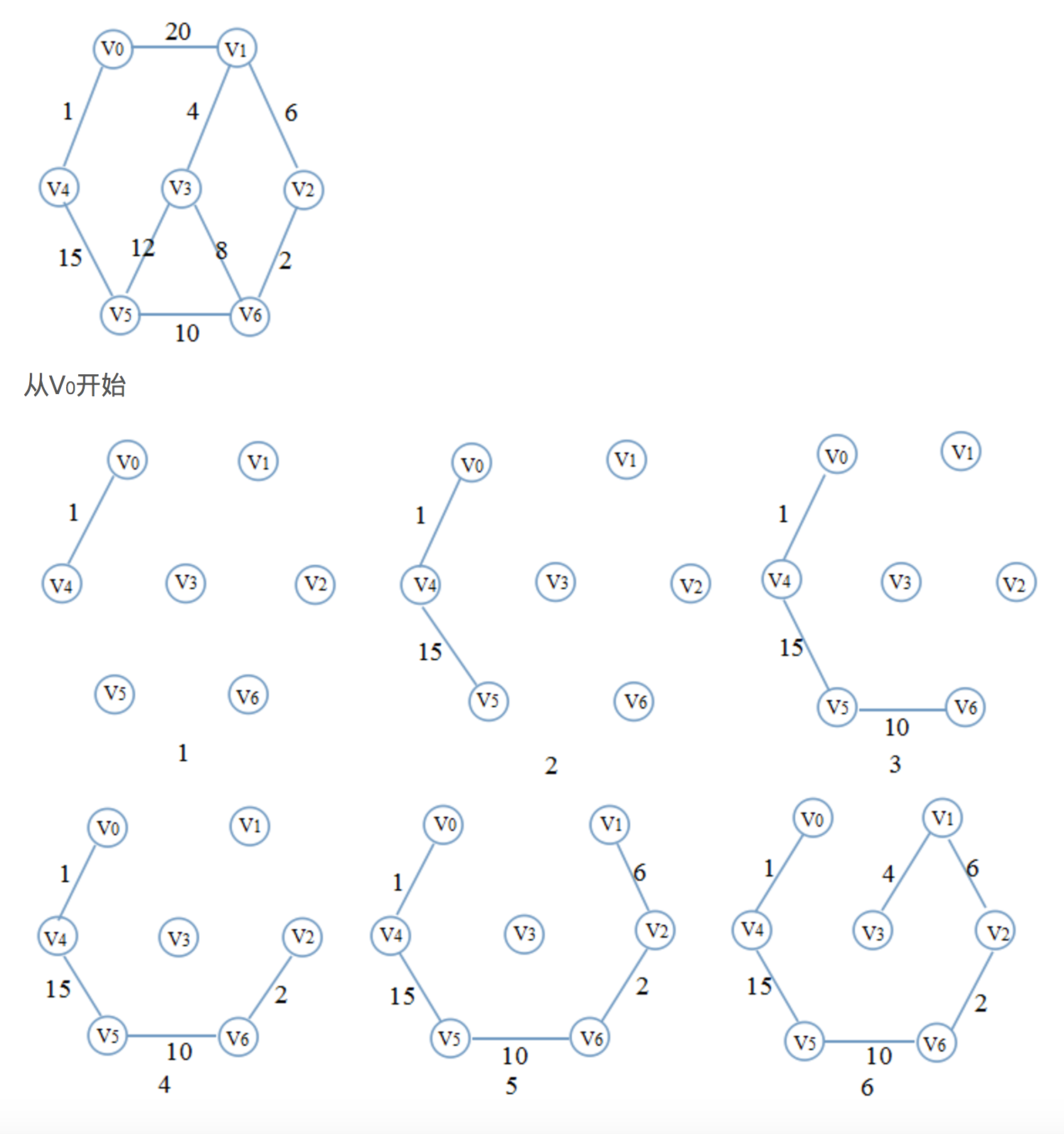
举例
题意:有S颗卫星和P个哨所,有卫星的两个哨所之间可以任意通信;否则,一个哨所只能和距离它小于等于D的哨所通信。给出卫星的数量和P个哨所的坐标,求D的最小值。
分析:这是一个最小生成树问题。P个哨所最多用P-1条边即可连起来,而S颗卫星可以代替S-1条边,基于贪心思想,代替的边越长,求得的D就越小。所以可以用一个数组保存加入最小生成树的边的长度,共有P-1条边,把前S-1条较长的边代替掉,剩下的边中最长的即为所求,即d[(P-1) - (S-1) - 1] = d[P-S-1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn=500+10;
const int maxm=500*500+10;
struct Point
{
double x,y;
}points[maxn];
struct Edge
{
int u,v;
double dist;//距离
Edge(){}
Edge(int u,int v,double d):u(u),v(v),dist(d){}
bool operator<(const Edge&rhs)const
{
return dist <rhs.dist;
}
}edges[maxm];
int n;
int fa[maxn];//并查集相关
int findset(int x){ return fa[x]==-1? x: fa[x]=findset(fa[x]); }
double get_dist(int i,int j)//勾股定理求两点之间的直线距离
{
double x1=points[i].x, y1=points[i].y, x2=points[j].x, y2=points[j].y;
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int main()
{
int T,S; scanf("%d",&T);
while(T--)
{
scanf("%d%d",&S,&n);
memset(fa,-1,sizeof(fa));
for(int i=0;i<n;i++)//记录每个村庄的坐标
scanf("%lf%lf",&points[i].x,&points[i].y);
int cnt=0;//边总数
for(int i=0;i<n;i++)
for(int j=i+1;j<n;j++)
{
edges[cnt++]=Edge(i,j,get_dist(i,j));//预处理求得所有的边
}
sort(edges,edges+cnt);//按kruskal算法对边排序
//添加n-S条有效边后,整个图还剩S个连通分量
int num=0; //当前添加的最小生成树边 数目
double D;
for(int i=0;i<cnt;i++)
{
int u=edges[i].u , v=edges[i].v;
if(findset(u) != findset(v))//两点没在同一连通分量中
{
fa[findset(u)] = findset(v);
if(++num == n-S) { D=edges[i].dist; break;}
//最小生成树中的最长k-1条长边都去掉后,正好将原树分成了k 个连通分支,在每个连通分支上摆一个卫星设备即可
//一个图的两棵最小生成树,边的权值序列排序后结果相同
}
}
printf("%.2lf\n",D);
}
return 0;
}
|


