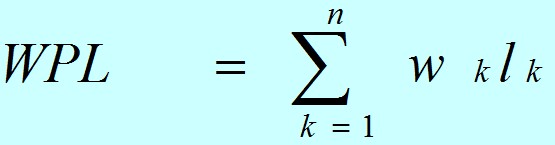一、哈夫曼树的定义

什么是哈夫曼树？

让我们先举一个例子。

判定树：

在很多问题的处理过程中，需要进行大量的条件判断，这些判断结构的设计直接影响着程序的执行效率。例如，编制一个程序，将百分制转换成五个等级输出。大家可能认为这个程序很简单，并且很快就可以用下列形式编写出来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


if(score<60)
    cout<<"Bad"<<endl;
else if(score<70)
    cout<<"Pass"<<endl
else if(score<80)
    cout<<"General"<<endl;
else if(score<90)
    cout<<"Good"<<endl;
else
    cout<<"Very good!"<<endl;

若考虑上述程序所耗费的时间，就会发现该程序的缺陷。在实际中，学生成绩在五个等级上的分布是不均匀的。当学生百分制成绩的录入量很大时，上述判定过程需要反复调用，此时程序的执行效率将成为一个严重问题。

但在实际应用中，往往各个分数段的分布并不是均匀的。下面就是在一次考试中某门课程的各分数段的分布情况：

下面我们就利用哈夫曼树寻找一棵最佳判定树，即总的比较次数最少的判定树。

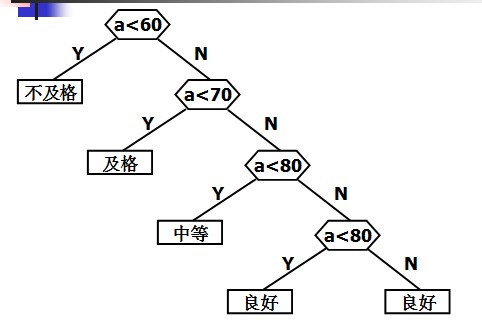
第一种构造方式：

第二种构造方式：

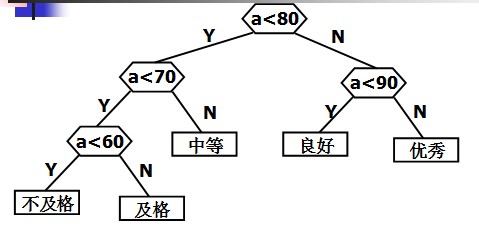
这两种方式，显然后者的判定过程的效率要比前者高。在也没有别地判定过程比第二种方式的效率更高。

我们称判定过程最优的二叉树为哈夫曼树，又称最优二叉树

二、哈弗曼树的性质

结点的带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值之积称为该结点的带权路径长度（weighted path length）

树的带权路径长度：如果树中每个叶子上都带有一个权值，则把树中所有叶子的带权路径长度之和称为树的带权路径长度。

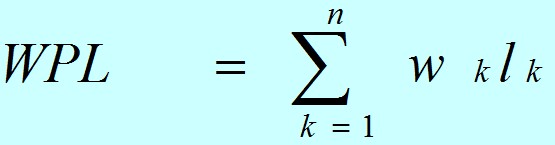
公式中，Wk为第k个叶子结点的权值；Lk为该结点的路径长度。

示例：

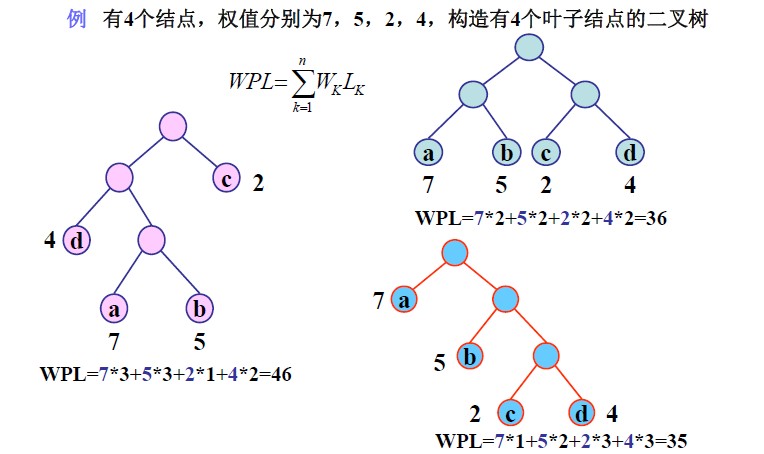
其中带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树.

性质：对于具有n个叶子节点的哈夫曼树，一共需要2*n-1个节点。

这个性质的解释如下：对于二叉树来说，有三种类型节点，即出度为2的节点，出度为1的节点和出度为0的叶节点。而哈夫曼树的非叶子节点是由两个节点生成的，因此不能出现度数为1的节点，而因为n个叶子节点需要进行n-1次构造才能成为哈弗曼树,所以非叶子节点的个数为叶子节点个数减1，于此定理就得证了。

性质:哈夫曼树的带权路径长度和所有非叶子结点的权值和相等.

三、哈弗曼树的构造

根据哈弗曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。

哈弗曼依据这一特点提出了一种构造最优二叉树的方法，其基本思想如下：

下面演示了用Huffman算法构造一棵Huffman树的过程：

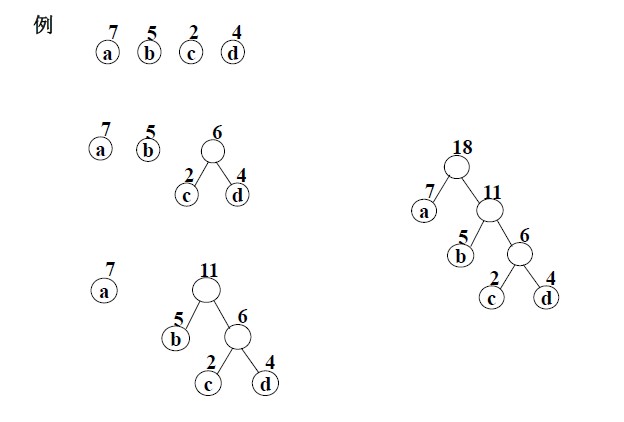
三、哈夫曼树的在编码中的应用

编码原则

在电文传输中，需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则：

（1）发送方传输的二进制编码，到接收方解码后必须具有唯一性，即解码结果与发送方发送的电文完全一样；

（2）发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。

等长编码这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。
不等长编码在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，1，01，并可将上述电文用二进制序列：000011010发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面4个0是4个A，1个B、2个A，还是2个B，即译码不唯一，因此这种编码方法不可使用。

因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀，这种编码称为前缀编码（prefix code）

哈弗曼编码

（1）利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；（2）从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码

例题：

有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

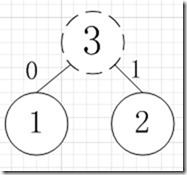
虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

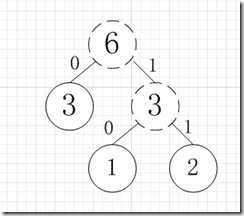
再依次建立哈夫曼树，如下图：

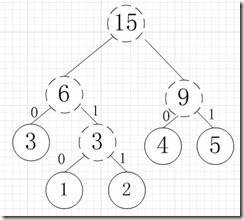
其中各个权值替换对应的字符即为下图：

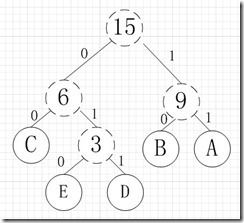
所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

代码实现

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117


#include <iostream>
#include <queue>
#include <string.h>
#include <vector>
#include <algorithm>
using namespace std;

char Table[26];

struct Node
{
    int     freq;
    char    val;
    Node    * left;
    Node    * right;
    Node():left(NULL), right(NULL) , freq(0) , val('0'){}
};

class Cmp
{
public:
    bool operator() (const Node * a, const Node * b) const
    {
        return  a->freq > b->freq;  // 从小到大 ，freq 小的 优先级别高
    }
};

priority_queue<Node* , vector<Node*> , Cmp> myQueue;

void BuildTree()
{
    for (int i = 0; i < 26; ++ i)
    {
        if (Table[i] > 0)
        {
            Node * node = new Node();
            node->freq = Table[i];
            node->val =(char) (i + 'A');
            myQueue.push(node);
        }
    }

    while (myQueue.size()>1)
    {
        Node * f = myQueue.top();
        myQueue.pop();
        Node * s = myQueue.top();
        myQueue.pop();
        Node * tmp = new Node();
        tmp->freq = f->freq + s->freq;
        tmp->left = f;
        tmp->right = s;
        myQueue.push(tmp);
    }
}

struct PrintNode
{
    int freq;
    char val;
    string code;
};

vector<PrintNode> vpn;
bool cmp(const PrintNode & a , const PrintNode & b)
{
    return a.freq > b.freq;
}

void Print( Node * node , string res)
{
    if (node == NULL)
    {
        return;
    }
    if (node->val != '0')  //如果不是'0',说明该节点代表了字符,而不是一个空的带权节点,需要存入vpn结果数组中
    {
        PrintNode pn;
        pn.val = node->val;
        pn.freq = node->freq;
        pn.code = res;
        vpn.push_back(pn);
        return ;
    }
    Print(node->left , res + "0");
    Print(node->right, res + "1");
    delete node->left;
    delete node->right;
}

int main()
{
    int N;
    memset(Table , 0 , sizeof(Table));
    cin >> N;
    for (int i = 0; i < N; ++i)
    {
        char ch ;
        cin >> ch;
        if (ch >= 'A' && ch <= 'Z')
        {
            ++Table[ch - 'A'];
        }
    }
    BuildTree();
    Node * root = myQueue.top();
    myQueue.pop();
    Print(root , "");

    sort(vpn.begin() , vpn.end() , cmp);

    for (int i = 0; i < vpn.size(); ++i)
    {
        cout <<vpn[i].val << " "<<vpn[i].freq <<" " << vpn[i].code<<endl;
    }
    return 0;
}

哈夫曼编码长度(总费用)

哈夫曼编码总长度也就是哈弗曼树的带权路径和,如果只求编码长度的话不需要构造哈弗曼树,直接用优先队列就可以求出.

性质:哈夫曼编码长度为哈弗曼树中所有非叶子结点的权值和.

例1:

搬水果

题目描述：

在一个果园里，小明已经将所有的水果打了下来，并按水果的不同种类分成了若干堆，小明决定把所有的水果合成一堆。每一次合并，小明可以把两堆水果合并到一起，消耗的体力等于两堆水果的重量之和。当然经过 n‐1 次合并之后，就变成一堆了。小明在合并水果时总共消耗的体力等于每次合并所耗体力之和。

假定每个水果重量都为 1，并且已知水果的种类数和每种水果的数目，你的任务是设计出合并的次序方案，使小明耗费的体力最少，并输出这个最小的体力耗费值。例如有 3 种水果，数目依次为 1，2，9。可以先将 1，2 堆合并，新堆数目为3，耗费体力为 3。然后将新堆与原先的第三堆合并得到新的堆，耗费体力为 12。所以小明总共耗费体力=3+12=15，可以证明 15 为最小的体力耗费值。

输入：

每组数据输入包括两行,第一行是一个整数 n(1<=n<=10000),表示水果的种类数，如果 n 等于 0 表示输入结束，且不用处理。第二行包含 n 个整数，用空格分隔，第 i 个整数(1<=ai<=1000)是第 i 种水果的数目。

输出：

对于每组输入，输出一个整数并换行，这个值也就是最小的体力耗费值。输入数据保证这个值小于 2^31。

样例输入：

3
9 1 2
0

样例输出：

编码:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


#include <iostream>
#include <queue>

using namespace std;

priority_queue<int,vector<int>,greater<int> >Q;

int main()
{
    int n;
    while(cin>>n){
        if(n==0)
            break;
        while(Q.empty()==false){
            Q.pop();
        }
        for(int i=1;i<=n;i++){
            int x;
            cin>>x;
            Q.push(x);
        }
        int ans=0;
        while(Q.size()>1){
            int a=Q.top();
            Q.pop();
            int b=Q.top();
            Q.pop();
            ans=ans+a+b;
            Q.push(a+b);
        }
        cout<<ans<<endl;
    }
    return 0;
}

例2:

题目描述

请设计一个算法，给一个字符串进行二进制编码，使得编码后字符串的长度最短。

输入描述:

每组数据一行，为待编码的字符串。保证字符串长度小于等于1000。

输出描述:

一行输出最短的编码后长度。

输入

MT-TECH-TEAM

输出

编码:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
char s[1005];
int main(){
    while(scanf("%s",s) != EOF){
        int n = strlen(s);
        sort(s,s + n);//利用排序来规避hash表求权值的过程,节约时间和空间
        priority_queue<int,vector<int>,greater<int> > heap;
        int cnt = 0;
        for(int i = 0,j;i < n;){
            j = i;
            while(j < n && s[j] == s[i]) ++ j;
            heap.push(j-i);
            i = j;
            ++ cnt;//记录叶子节点个数
        }
        int ret = 0;
        for(int i = 0;i < cnt - 1;++ i){//cnt-1个非叶子结点
            int A = heap.top(); heap.pop();
            int B = heap.top(); heap.pop();
            ret += A + B;
            heap.push(A + B);
        }  
        printf("%d\n",ret);
    }
    return 0;
}

哈弗曼树详解

文章目录