哈希算法与哈希表介绍

哈希算法

下面简单介绍下几种比较常用的加密哈希算法：

MD5

MD5 即 Message-Digest Algorithm 5（信息-摘要算法 5），用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一，主流编程语言普遍已有 MD5 实现。将数据（如汉字）运算为另一固定长度值，是杂凑算法的基础原理，MD5 的前身有 MD2、MD3 和 MD4。

MD5 是输入不定长度信息，输出固定长度 128-bits 的算法。经过程序流程，生成四个 32 位数据，最后联合起来成为一个 128-bits 散列。基本方式为，求余、取余、调整长度、与链接变量进行循环运算。得出结果。 NodeJS 中使用 MD5：

1
2
3
4
5
6


var hash = crypto.createHash('md5');
hash.update('test');
console.log(hash.digest('hex'));    // 098f6bcd4621d373cade4e832627b4f6
var hash = crypto.createHash('md5');
hash.update('test1');
console.log(hash.digest('hex'));    // 5a105e8b9d40e1329780d62ea2265d8a

MD5 一度被广泛应用于安全领域。但是在 2004 年王小云教授公布了 MD5、MD4、HAVAL-128、RIPEMD-128 几个 Hash 函数的碰撞。这是近年来密码学领域最具实质性的研究进展。使用他们的技术，在数个小时内就可以找到 MD5 碰撞。使本算法不再适合当前的安全环境。目前，MD5 计算广泛应用于错误检查。例如在一些 BitTorrent 下载中，软件通过计算 MD5 和检验下载到的碎片的完整性。

SHA-1

SHA-1 曾经在许多安全协议中广为使用，包括 TLS 和 SSL、PGP、SSH、S/MIME 和 IPsec，曾被视为是 MD5 的后继者。 SHA-1 是如今很常见的一种加密哈希算法，HTTPS 传输和软件签名认证都很喜欢它，但它毕竟是诞生于 1995 年的老技术了 (出自美国国安局 NSA)，已经渐渐跟不上时代，被破解的速度也是越来越快。微软在 2013 年的 Windows 8 系统里就改用了 SHA-2，Google、Mozilla 则宣布 2017 年 1 月 1 日起放弃 SHA-1。当然了，在普通民用场合，SHA-1 还是可以继续用的，比如校验下载软件之类的，就像早已经被淘汰的 MD5。

1
2
3


var hash = crypto.createHash('sha1');
hash.update('test');
console.log(hash.digest('hex'));    // a94a8fe5ccb19ba61c4c0873d391e987982fbbd3

SHA-2

SHA-224、SHA-256、SHA-384，和 SHA-512 并称为 SHA-2。

新的哈希函数并没有接受像 SHA-1 一样的公众密码社区做详细的检验，所以它们的密码安全性还不被大家广泛的信任。虽然至今尚未出现对 SHA-2 有效的攻击，它的算法跟 SHA-1 基本上仍然相似；因此有些人开始发展其他替代的哈希算法。

1
2
3


var hash = crypto.createHash('sha256');
hash.update('test');
console.log(hash.digest('hex'));    // 9f86d081884c7d659a2feaa0c55ad015a3bf4f1b2b0b822cd15d6c15b0f00a08

SHA-3

SHA-3，之前名为 Keccak 算法，是一个加密杂凑算法。由于对 MD5 出现成功的破解，以及对 SHA-0 和 SHA-1 出现理论上破解的方法，NIST 感觉需要一个与之前算法不同的，可替换的加密杂凑算法，也就是现在的 SHA-3。

RIPEMD-160

RIPEMD-160 是一个 160 位加密哈希函数。它旨在用于替代 128 位哈希函数 MD4、MD5 和 RIPEMD。 RIPEMD-160 没有输入大小限制，在处理速度方面比 SHA2 慢。安全性也没 SHA-256 和 SHA-512 好。

1
2
3


var hash = crypto.createHash('ripemd160');
hash.update('test');
console.log(hash.digest('hex'));    // 5e52fee47e6b070565f74372468cdc699de89107

查找哈希算法

下面列举几个目前在查找方面比较快的哈希算法（不区分先后），比较老的或者慢的就没举例了，毕竟篇幅有限。

lookup3

Bob Jenkins 在 1997 年发表了一篇关于哈希函数的文章《A hash function for hash Table lookup》，这篇文章自从发表以后现在网上有更多的扩展内容。这篇文章中，Bob 广泛收录了很多已有的哈希函数，这其中也包括了他自己所谓的 “lookup2”。随后在 2006 年，Bob 发布了 lookup3。

Bob 很好的实现了散列的均匀分布，但是相对来说比较耗时，它有两个特性，1 是具有抗篡改性，既更改输入参数的任何一位都将带来一半以上的位发生变化，2 是具有可逆性，但是在逆运算时，它非常耗时。

Murmur3

murmurhash 是 Austin Appleby 于 2008 年创立的一种非加密哈希算法，适用于基于哈希进行查找的场景。murmurhash 最新版本是 MurMurHash3，支持 32 位、64 位及 128 位值的产生。 MurMur 经常用在分布式环境中，比如 Hadoop，其特点是高效快速，但是缺点是分布不是很均匀。

设想这样的场景：当数据中有几个字段相同，就可以把它当作同类型数据。对于同类型的数据，我们需要做去重。

一个通常的解决办法是，使用 MD5 计算这几个字段的指纹，然后把指纹存起来。如果当前指纹存在，则表示有同类型的数据。

这种情况下，由于不涉及故意的哈希碰撞，并不一定要采用加密哈希算法。（加密哈希算法的一个特点是，即使你知道哈希值，也很难伪造有同样哈希值的文本）

而非加密哈希算法通常要比加密哈希算法快得多。如果数据量小，或者不太在意哈希碰撞的频率，甚至可以选择生成哈希值小的哈希算法，占用更小的空间。

就个人而言，我偏好在这种场景里采用 MurMurHash3，128 位的版本。理由有三：

MurMurHash3 久经沙场，主流语言里面都能找到关于它的库。
MurMurHash3，128 位版本的哈希值是 128 位的，跟 MD5 一样。128 位的哈希值，在数据量只有千万级别的情况下，基本不用担心碰撞。
MurMurHash3 的计算速度非常快。

MurMurHash3 哈希算法是 MurMurHash 算法家族的最新一员。虽说是“最新一员”，但距今也有五年的历史了。无论从运算速度、结果碰撞率，还是结果的分布均衡程度进行评估，MurMurHash3 都算得上一个优秀的哈希算法。

除了 128 位版本以外，它还有生成 32 位哈希值的版本。在某些场景下，比如哈希的对象长度小于 128 位，或者存储空间要求占用小，或者需要把字符串转换成一个整数，这一特性就能帮上忙。当然，32 位哈希值发生碰撞的可能性就比 128 位的要高得多。当数据量达到十万时，就很有可能发生碰撞。

MurMurHash3 128 位版本的速度是 MD5 的十倍。有趣的是，MurMurHash3 生成 32 位哈希的用时比生成 128 位哈希的用时要长。原因在于生成 128 位哈希的实现受益于现代处理器的特性。

FNV-1a

FNV 又称 Fowler/Noll/Vo，来自 3 位算法设计者的名字（Glenn Fowler、Landon Curt Noll 和 Phong Vo）。FNV 有 3 种：FNV-0（已过时）、FNV-1、FNV-1a，后两者的差别极小。FNV-1a 生成的哈希值有几个特点：无符号整形；哈希值的 bits 数，是 2 的 n 次方（32, 64, 128, 256, 512, 1024），通常 32 bits 就能满足大多数应用。

跟 FNV 的初次邂逅，是在 Go 的标准库文档里。我很惊讶，一门主流语言的标准库里，居然会有不太知名的哈希算法。从另一个角度看，非加密哈希算法还是有其必要性的，不然 Go 这门以实用著称的语言也不会内置 FNV 算法了。

可惜跟其他哈希算法相比，FNV 并无出彩之处（参考 SMHasher 测试结果）。FNV 家族较新的 FNV-1a 版本，对比于 FNV-1 做了一些改善。尽管如此，除非写的是 Go 程序，我通常都不会考虑使用它。

CityHash

2011 年，google 发布 CityHash（由 Geoff Pike 和 Jyrki Alakuijala 编写）, 其性能好于 MurmurHash。

但后来 CityHash 的哈希算法被发现容易受到针对算法漏洞的攻击，该漏洞允许多个哈希冲突发生。

SpookyHash

又是 Bob Jenkins 哈希牛人的一巨作，于 2011 年发布的新哈希函数性能优于 MurmurHash，但是只给出了 128 位的输出，后面发布了 SpookyHash V2，提供了 64 位输出。

FarmHash

FarmHash 也是 google 发布的，FarmHash 从 CityHash 继承了许多技巧和技术，是它的后继。FarmHash 声称从多个方面改进了 CityHash。

xxhash

xxhash 由 Yann Collet 发表，http://cyan4973.github.io/xxHash/ 这是它的官网，据说性能很好，似乎被很多开源项目使用，Bloom Filter 的首选。

查找哈希函数的性能比较

一般性能好的哈希算法都会根据不同系统做优化。

这里有一篇文章详细介绍了各种非加密哈希的性能比较（http://aras-p.info/blog/2016/08/09/More-Hash-Function-Tests/）。

文章详细列出了各个平台（甚至包括手机和 XBOXOne 以及 asm.js）之间的哈希算法性能比较，同时也对不同输入数据量做了对比。

似乎在跨平台使用方面 CityHash64 在 64 位系统性能最佳，而 xxHash32 在 32 位系统性能最好。

在数据量大方面，不同平台也有不同的选择

Intel CPU：总体来说 xxhash64 更好，随之 FarmHash64（如果使用了 SSE4.2），xxHash32 更适合 32 位系统。

苹果手机 CPU（A9）：CityHash64 在 64 位系统性能最佳，而 xxHash32 在 32 位系统性能最好。

SpookyV2 更适合在 XBOXOne 中使用。

而短字符串输入使用 FNV-1a 性能最优（在 pc，手机和 XBOX 中少于 8 字节，在 asm.js 中少于 20 字节），而且它的实现很简单。

哈希函数的分类

介绍了那么多哈希函数，实际上哈希函数主要分为以下几类：

1、加法 Hash；所谓的加法 Hash 就是把输入元素一个一个的加起来构成最后的结果，prime 是素数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


function addictiveHash(key = '', prime){
    let hash = 0;
    for(let i = 0; i < key.length; ++i){
        hash += key.charCodeAt(i);
    }

    return hash % prime;
}

console.log(addictiveHash('test', 31)); // 14
console.log(addictiveHash('abc', 31)); // 15
console.log(addictiveHash('abb', 31)); // 14

2、位运算 Hash；这类型 Hash 函数通过利用各种位运算（常见的是移位和异或）来充分的混合输入元素。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


function rotatingHash(key = '', prime) {
    let hash = 0;
    for (let i = 0; i < key.length; ++i) {
        hash = (hash << 4) ^ (hash >> 28) ^ key.charCodeAt(i);
    }
    return (hash % prime);
}
console.log(rotatingHash('test', 31)); // 13
console.log(rotatingHash('abc', 31)); // 23
console.log(rotatingHash('abb', 31)); // 22

3、乘法 Hash；

这样的类型的哈希函数利用了乘法的不相关性. 乘法哈希里最有名的就是 adler32，reactJS 的 checksum 校验就是使用的 adler32 的改良版。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


function adler32(str) {
    var a = 1, b = 0, L = str.length, M = 0, c = 0, d = 0;

    for (var i = 0; i < L;) {
        M = Math.min(L - i, 3850);
        while (M > 0) {
            c = str.charCodeAt(i++);
            if (c < 0x80) { a += c; }
            else if (c < 0x800) {
                a += 192 | ((c >> 6) & 31); b += a; --M;
                a += 128 | (c & 63);
            } else if (c >= 0xD800 && c < 0xE000) {
                c = (c & 1023) + 64; d = str.charCodeAt(i++) & 1023;
                a += 240 | ((c >> 8) & 7); b += a; --M;
                a += 128 | ((c >> 2) & 63); b += a; --M;
                a += 128 | ((d >> 6) & 15) | ((c & 3) << 4); b += a; --M;
                a += 128 | (d & 63);
            } else {
                a += 224 | ((c >> 12) & 15); b += a; --M;
                a += 128 | ((c >> 6) & 63); b += a; --M;
                a += 128 | (c & 63);
            }
            b += a; --M;
        }
        a = (15 * (a >>> 16) + (a & 65535));
        b = (15 * (b >>> 16) + (b & 65535));
    }
    return ((b % 65521) << 16) | (a % 65521);
}
console.log(adler32('test', 31)); // 73204161
console.log(adler32('abc', 31)); // 38600999
console.log(adler32('abb', 31)); // 38535462

4、除法 Hash；和乘法一样用了不相关性，但性能不好。

5、查表 Hash；查表 Hash 最有名的样例莫过于 CRC 系列算法。尽管 CRC 系列算法本身并非查表，可是，查表是它的一种最快的实现方式。以下是 CRC32 的实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


function signed_crc_table() {
    var c = 0, table = new Array(256);

    for(var n =0; n != 256; ++n){
        c = n;
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        c = ((c&1) ? (-306674912 ^ (c >>> 1)) : (c >>> 1));
        table[n] = c;
    }

    return typeof Int32Array !== 'undefined' ? new Int32Array(table) : table;
}

var T = signed_crc_table();
function crc32(str, seed) {
    var C = seed ^ -1;
    for(var i = 0, L=str.length, c, d; i < L;) {
        c = str.charCodeAt(i++);
        if(c < 0x80) {
            C = (C>>>8) ^ T[(C ^ c)&0xFF];
        } else if(c < 0x800) {
            C = (C>>>8) ^ T[(C ^ (192|((c>>6)&31)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|(c&63)))&0xFF];
        } else if(c >= 0xD800 && c < 0xE000) {
            c = (c&1023)+64; d = str.charCodeAt(i++)&1023;
            C = (C>>>8) ^ T[(C ^ (240|((c>>8)&7)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|((c>>2)&63)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|((d>>6)&15)|((c&3)<<4)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|(d&63)))&0xFF];
        } else {
            C = (C>>>8) ^ T[(C ^ (224|((c>>12)&15)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|((c>>6)&63)))&0xFF];
            C = (C>>>8) ^ T[(C ^ (128|(c&63)))&0xFF];
        }
    }
    return C ^ -1;
}
console.log(crc32('test', 31)); // -804963899
console.log(crc32('abc', 31)); // 576628111
console.log(crc32('abb', 31)); // 1431934233

查表 Hash 中有名的样例有：Universal Hashing 和 Zobrist Hashing。他们的表格都是随机生成的。

6、混合 Hash；混合 Hash 算法利用了以上各种方式。各种常见的 Hash 算法，比方 MD5、Tiger 都属于这个范围。它们一般非常少在面向查找的 Hash 函数里面使用。

哈希函数的选择

那么多种哈希函数，我们究竟该选择哪种呢？不同的应用场景对哈希的算法设计要求也不一样，但一个好的哈希函数应该具备以下三点：

抗碰撞性，尽量避免冲突。
抗篡改性，只要改动一个字节，其哈希值也会很大不同。
查找效率。

在加密方面，哈希函数应该对抗碰撞性和抗篡改性要求很高，而会牺牲查找效率。而且随着时代的变化我们最好还是选择更现代化的哈希函数。目前来说我们可以选择 SHA-2 族用于安全加密中，SHA-3 更安全但对性能损耗更大。更保险的做法是加盐后混合加密。在 nodejs 中我们可以很方便地用 crypto.pbkdf2() 函数加盐加密，默认会调用 hmac 算法，用 sha-1 进行加密，并且可以设置迭代次数和密文长度。常用于用户注册和登录校验流程中。下面的例子我们用伪随机函数 randomBytes() 生成 16 字节的盐（更安全的做法是多于 16 字节）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


const crypto = require('crypto');

let txt = 'test';

//通过伪随机码生成salt，进行加密
crypto.randomBytes(128, function (err, salt) {
    if (err) throw err;
    salt = salt.toString('hex');
    console.log(salt); //生成salt

    crypto.pbkdf2(txt, salt, 4096, 256, function (err,hash) {
        if (err) throw err;
        hash = hash.toString('hex');
        console.log(hash);//生成密文
    })
})

/*
6e5e20869916c5aea5f6188807abb0dcd83ca0d3c21ec880bab71c483e7cca624af8c5b6fe2ec820e296452e6e43476
98411aa545d4c3a21056e02659446b694383b3eedd3a7cbcb9592ede2d5875206f6b764fee69e65271c99d73b818837
9d0c92e345b046d760b84954babd6740b6928e76ef86e9bfd07c2867837678b575
(node:1264) DeprecationWarning: crypto.pbkdf2 without specifying a digest is deprecated. Please
 specify a digest
4572e319f6f5e05ee2507dacc43cd9c6f970e1ed37e76c2a86c99afde11c75f35f04322ee3fec4775a21f1181c0e357
d00bdf1f1aef4cffe9f11f7859fea658df76553ae37deacc5e085d5e7e38a13ec0f7b0d8f29d738f0cd00cddbd74493
53547eb651244a6c3e599d86878f80e1be2d269afd3d9ea678982150163fa9e61385f40fabedae2403085e8432a723e
da8693466068523c9e26afdd0764a21d2372bde7f607af6bcbc8fd4a325ad942688ee770efdf038332a470b7ed7c49e
7c9b0f8d6a1f9557dd51c3747ac4a7ecabda7089d5685403e6af525de5f84d0b4d7a53ea1fb879afa2cfee4a60775b5
39614ef451de2dd1ca995a14a79c4236d6089
*/

而在查找方面，哈希函数更追求查找的效率和良好的抗碰撞性。

短字符串输入使用 FNV-1a，数量大的在 32 位系统使用 xxhash，64 位系统使用 FarmHash。

哈希表

hash table可提供对任何有名项（nameditem)的存取操作和删除操作。由于操作对象是有名项，所以hashtable也可被视为一种字典结构（dictionary)。这种结构的用意在于提供常数时间之基本操作，就像stack或queue那样。

举个例子，如果所有的元素都是16-bits且不带正负号的整数，范围0~65535,那么简单地运用一个array就可以满足上述期望。首先配置一个array A,拥有65536个元素，索引号码0〜65535,初值全部为0,如图5-21。每一个元素值代表相应元素的出现次数。如果插入元素i,我们就执行A[i]++,如果删除元素i,我们就执行A[i]–，如果搜寻元素i，我们就检查A[i]是否为0。以上的每一个操作都是常数时间。

这种解法的额外负担是array的空间和初始化时间。

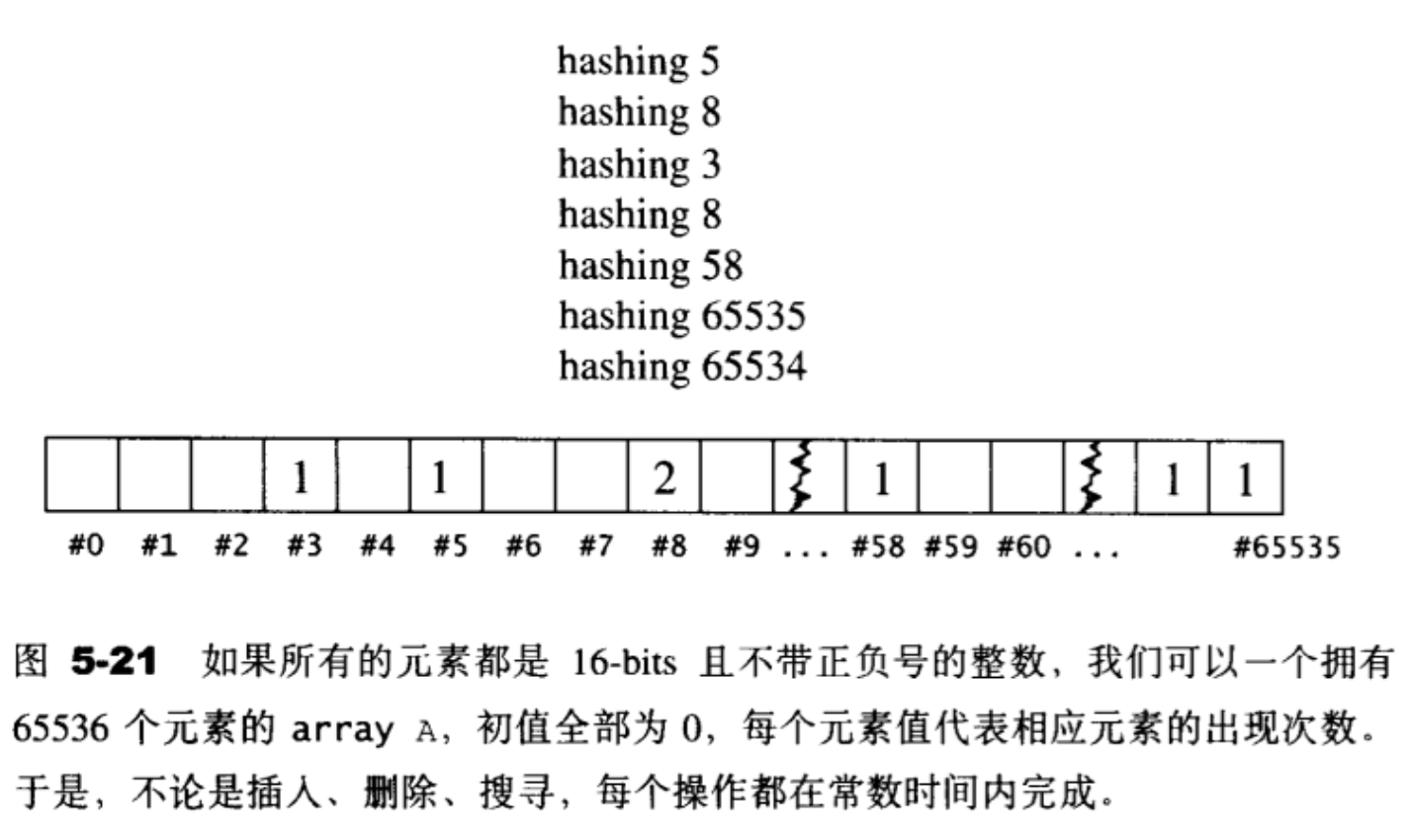
这个解法存在两个现实问题。

第一，如果元素是32-bits而非16-bits，我们所准备的array A的大小就必须是2^32=4GB，这就大得不切实际了。第二，如果元素型态是字符串（或其它）而非整数，将无法被拿来作为array的索引。

第二个问题（关于索引）不难解决。就像数值1234是由阿拉伯数字1,2,3,4 构成一样，字符串"jjhou"是由字符构成。那么，既然数值1234是我们也可以把字符编码，每个字符以一个7-bits数值来表示（也就是ASCII编码），从而将字符串"jjhou”表现为:

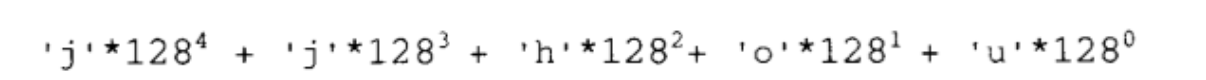
于是先前的array实现法就可适用于“元素型别为字符串”的情况了。但这并不实用，因为这会产生出非常巨大的数值。“jjhou"的索引值将是：

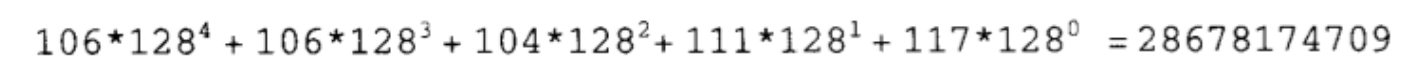
这太不切实际了。更长的字符串会导致更大的索引值!这就回归到第一个问题:array的大小。

如何避免使用一个大得荒谬的array呢？办法之一就是使用某种映射函数，将大数映射为小数。负责将某一元素映射为一个“大小可接受之索引”，这样的函数称为hash function(散列画数）.例如，假设x是任意整数，TableSize是array大小，则X%TableSize会得到一个整数，范围在0 ~ TableSize-1之间，恰可作为表格（也就是array)的索引。

使用hash function会带来一个问题：可能有不同的元素被映射到相同的位置(亦即有相同的索引）。这无法避免，因为元素个数大于array容量。这便是所谓的“碰撞（collision) ”问题。解决碰撞问题的方法有许多种，包括线性探测（linear probing)、二次探测（quadraticprobing)、开链（separatechaining)…等做法。每一种方法都很容易，导出的效率各不相同,与array的填满程度有很大的关连。

线性探测（linear probing)

首先让我们认识一个名词：负载系数（loading factor)，意指元素个数除以表格大小。负载系数永远在0〜1之间,除非采用开链（separatechaining)策略，后述。

当hash function计算出某个元素的插入位置，而该位置上的空间已不再可用时，我们应该怎么办？最简单的办法就是循序往下一一寻找（如果到达尾端，就绕到头部继续寻找），直到找到一个可用空间为止。只要表格（亦即array)足够大，总是能够找到一个安身立命的空间，但是要花多少时间就很难说了。进行元素搜寻操作时，道理也相同，如果hashfimctiori计算出来的位置上的元素值与我们的搜寻目标不符，就循序往下一一寻找，直到找到吻合者，或直到遇上空格元素。至于元素的删除，必须采用惰性删除（lazy deletion) 也就是只标记删除记号，实际删除操作则待表格重新整理（rehashing)时再进行——这是因为hash table中的每一个元素不仅表述它自己，也关系到其它元素的排列。

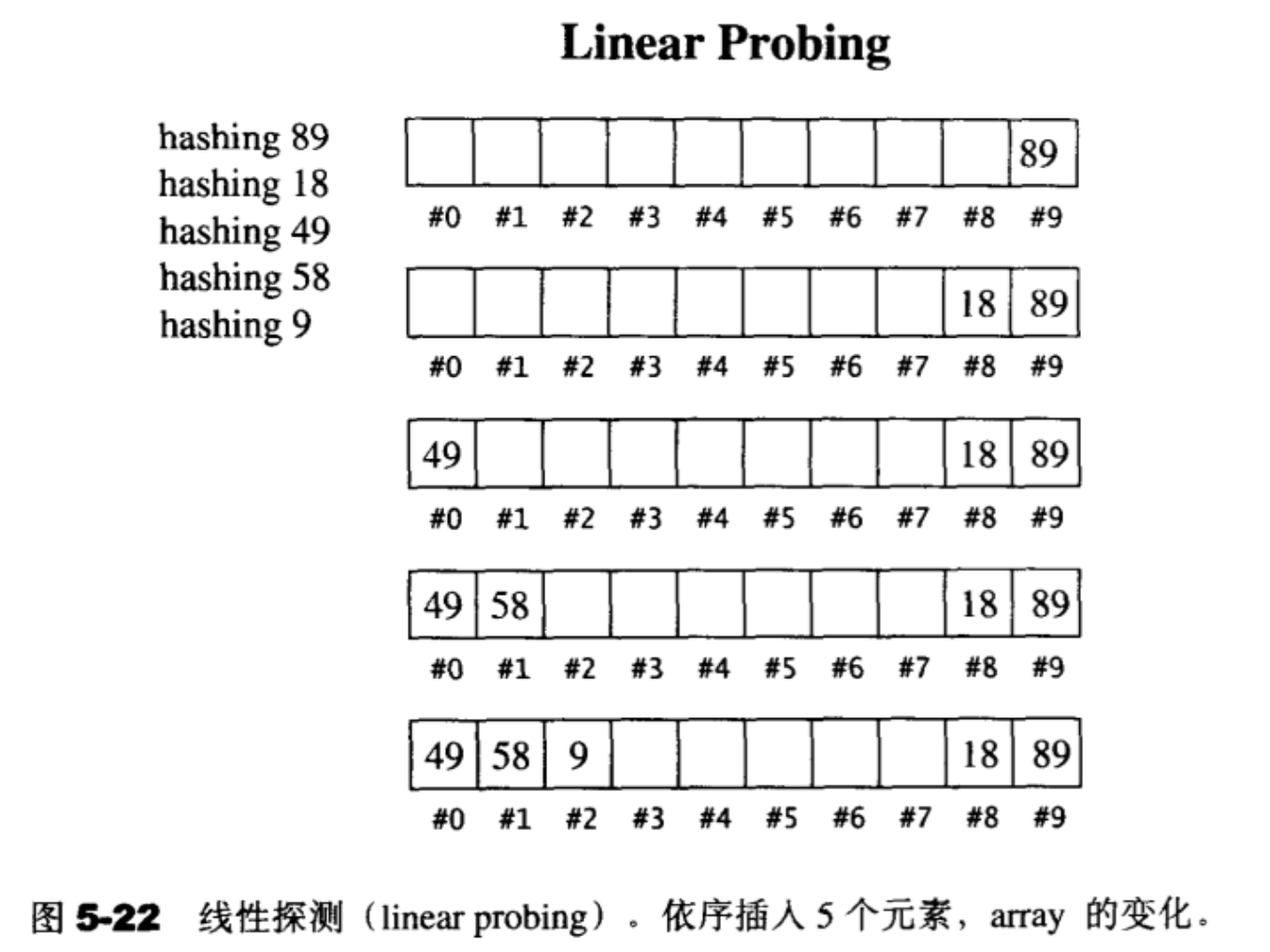
欲分析线性探测的表现，需要两个假设：（1)表格足够大；（2)每个元素都够独立。在此假设之下，最坏的情况是线性巡访整个表格，平均情况则是巡访一半表格，这已经和我们所期望的常数时间天差地远了，而实际情况犹更糟糕。问题出在上述第二个假设太过于天真。

拿实际例子来说，接续最后状态，除非新元素经过hash function的计算之后直接落在位置#4 ~ #7,否则位置#4〜#7永远不可能被运用，因为位置#3永远是第一考虑。换句话说，新元素不论是8,9,0，1，2,3中的哪一个，都会落在位置#3上。新元素如果是4或5，或6，或7，才会各自落在位置#4，或#5,或#6,或#7上。

这很清楚地突显了一个问题：平均插入成本的成长幅度，远高于负载系数的成长幅度。这样的现象在hashing过程中称为主集团（primary clustering)。

二次探测（quadratic probing)

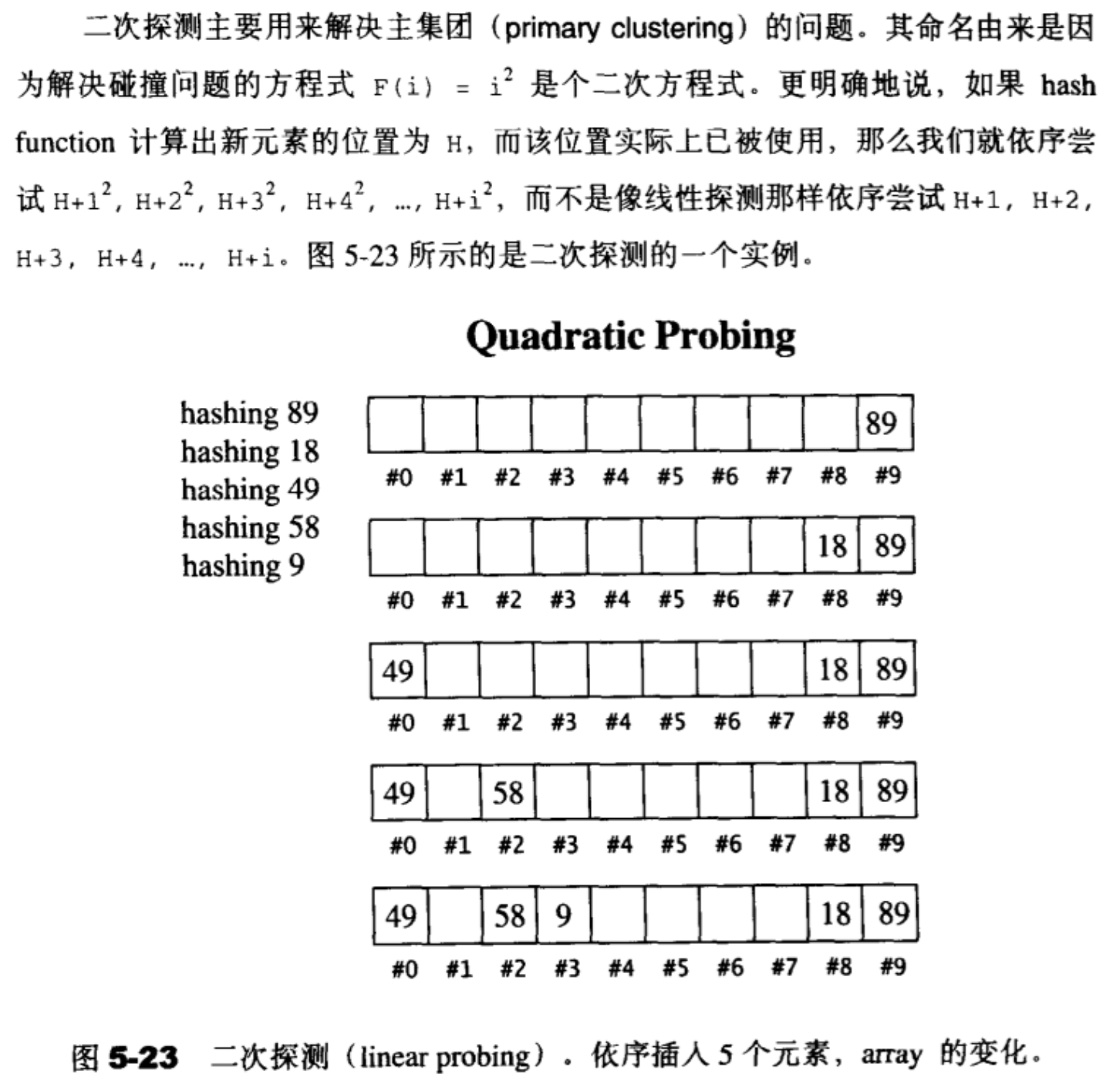
二次探测带来一些疑问：

线性探测法每次探测的都必然是一个不同的位置，二次探测法是否能够保证如此？二次探测法是否能够保证如果表格之中没有X，那么我们插入X一定能够成功？
线性探测法的运算过程极其简单，二次探测法则显然复杂得多。这是否会在执行效率上带来太多的负面影响？
不论线性探测或二次探测，当负载系数过高时，表格是否能够动态成长？

幸运的是，如果我们假设表格大小为质数（prime)，而且永远保持负载系数在0.5以下（也就是说超过0.5就重新配置并重新整理表格），那么就可以确定每插人一个新元素所需要的探测次数不多于2。

关键字是随机分布的，那么无所谓一定要模质数。但在实际中往往关键字有某种规律，例如大量的等差数列，那么公差和模数不互质的时候发生碰撞的概率会变大，而用质数就可以很大程度上回避这个问题。但质数并不是唯一的准则,参考good hash table primes

至于实现复杂度的问题，一般总是这样考虑：赚的比花的多，才值得去做。我们受累增加了探测次数，所获得的利益好歹总得多过二*次函数计算所多花的时间，不能吃肥走痩,得不偿失。线性探测所需要的是一个加法（加1)、一个测试（看是否需要绕转回头），以及一个偶需为之的减法（用以绕转回头）。二次探测需要的则是一个加法（从i-l到i)、一个乘法（计算i2),另一个加法，以及一个mod运算。看起来很有得不偿失之嫌。然而这中间却有一些小技巧，可以去除耗时的乘法和除法：

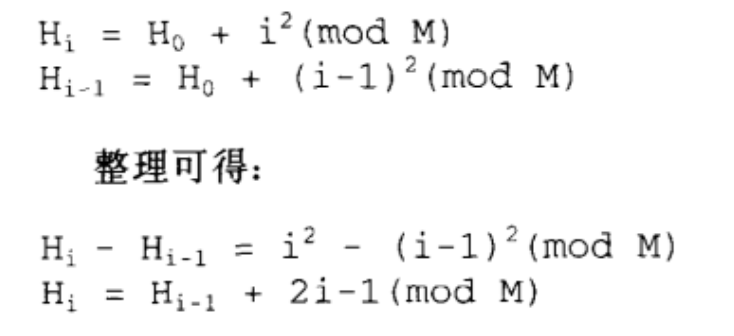
因此，如果我们能够以前一个H值来计算下一个H值，就不需要执行二次方所需要的乘法了。虽然还是需要一个乘法，但那是乘以2,可以位移位（bitshift)快速完成。至于mod运算，也可证明并非真有需要。

最后一个问题是array的成长。欲扩充表格，首先必须找出下一个新的而且够大（大约两倍）的质数，然后必须考虑表格重建（rehashing)的成本.不可能只是原封不动地拷贝而已，我们必须检验旧表格中的每一个元素，计算其在新表格中的位置，然后再插入到新表格中。

二次探测可以消除主集团（primary clustering)，却可能造成次集团（secondaryclustering):两个元素经hash function计算出来的位置若相同，则插人时所探测的位置也相同，形成某种浪费。消除次集团的办法当然也有，例如复式散列（double hashing)

虽然目前还没有对二次探测有数学上的分析，不过，以上所有考虑加加减减起来，总体而言，二次探测仍然值得投资。

开链(separate chaining)

另一种与二次探测法分庭抗礼的，是所谓的开链（separatechaining)法。这种做法是在每一个表格元素中维护一个list; hash function为我们分配某一个list，然后我们在那个list身上执行元素的插人、搜寻、删除等操作。虽然针对list而进行的搜寻只能是一种线性操作，但如果list够短，速度还是够快。

使用开链手法，表格的负载系数将大于1。STL的hash table便是采用这种做法.

Go使用xxHash

xxHash 是一种极快的非加密哈希算法，在 RAM 速度限制下工作。它提出了四种风格（XXH32、XXH64、XXH3_64bits 和 XXH3_128bits）。最新版本 XXH3 提供全面改进的性能，尤其是在小数据上。

xxh64:

1
2
3
4
5
6
7


package main

import "github.com/cespare/xxhash"

func main() {
	xxhash.Sum64String("aaa")
}

xxh3:

1
2
3
4
5
6
7


package main

import "github.com/zeebo/xxh3"

func main() {
	xxh3.Hash([]byte("star"))
}

参考

漫谈非加密哈希算法（MurMurHash，CRC32，FNV，SipHash，xxHash）

哈希函数介绍

文章目录