位图排序
文章目录
计数排序与位图排序
计数排序(Counting sort)是一种稳定的线性时间排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。计数排序不是比较排序,排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存。计数排序更适合于小范围集合的排序。比如100万学生参加高考,我们想对这100万学生的数学成绩(假设分数为0到100)做个排序。计数排序的步骤如下:
-
确定待排序数组中数值的范围,以此确定C数组的大小;
-
计算数组中每个值为A[i]的元素出现的次数,存入数组C[A[i]]中;
-
用C数组重新填充原数组。 需要注意几点:
-
计数排序是典型的以空间换时间,数组内元素的范围决定了伴随数组C的大小,从而决定程序运行的时间和内存大小。
-
计算C[i]时,使用了A[i]作为下标,那么必须保证A数组中所有元素非负,如果存在负值,那么可以对数组元素加上最小负值的绝对值,使得数组元素全部为正数。
位图排序
当计数排序中原数组A中数值范围较大时,伴随数组C也越大,内存的消耗越大,要进一步限制内存的大小,可以使用位图法(Bit-map)进行排序。假设要对数值范围为0-7内的5个数(4,7,2,5,3)进行排序,那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,如下图
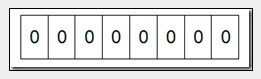
然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1,当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending),因为是从零开始的,所以要把第五位置为一(如下图):
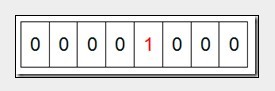
接着再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1,这时候的内存的Bit位的状态如下:
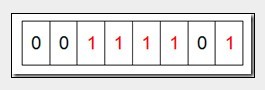
位图排序同样是一种线性排序,与计数排序相比,动态分配的伴随数组占用的空间小了很多,但是存在一个缺点,位图排序要求所排序的数组中没有重复元素,因为一个bit位只能用0,1来表示一个整数的存在与否,不能表示此整数数的出现次数.
位图法除了可以用作排序,也可以用来做匹配和查找。
类似题目
-
QQ号数字范围从0到十亿,即[0, 1000000000),且最多给你10亿个QQ号,这些QQ号放在1或多个文本文件中,格式是每行一个QQ号,怎样快速去除重复的QQ号?
设有char类型数x,1字节包括8个位,我们可以申请char bit_map[10亿/8+1]的空间,就足以给范围在[0,10亿)的数字去重了。
选择char类型而不是int等其它类型是考虑到,C标准规定任何实现都要保证char类型占1个字节。
+1,是考虑到C整型除法向下取整的特点,比如100/8结果为12,这样访问编号>=96的比特位(设从0开始编号),就会发生数组越界。
然后将每一个qq号看成一个int型数,在bit_map中给相应的位置赋1,如果发现已经为1,就说明该qq号是重复的。
-
一个最多包含n个正整数的文件,每个数都小于n,其中n=10^7,且所有正整数都不重复。求如何将这n个正整数升序排列。
约束:最多有1MB的内存空间可用,有充足的磁盘存储空间。
这个题目的最大亮点是只有1MB的内存空间,我们可以通过计算得出,内存只有1MB可以储存的int(4byte)有10^3*10^3/4=250 000个号码。而包含正整数的文件约为10^7个int大小。这意味着无法将所有文件中的正整数一次读取进入到内存空间中去进行排序算法。
位图法方法:
-
创建有10^7位(10^7/8/1024/1024≈1MB)的字符串,并将其每一bit设置为0;
-
读取包含正整数的文件,对每一个i,将内存中bit[i] 位设置成1.
-
按位顺序读取字符串。当读取到bit[j] 为1时输出(int)j。
-
-
给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中
unsign int范围为0~2^32-1(4294967295≈5*10^9) 使用位图hash对应5*10^9/8/10^3/10^3 = 625MB.
我们使用625M的字符串。每一位设置为0.
将40亿个unsign int 遍历一遍。使用位图法将字符串中的对应位转化为1。
读取“再给一个数i” 查看bit[i] 是否为1,1则有存在,0则不存在。
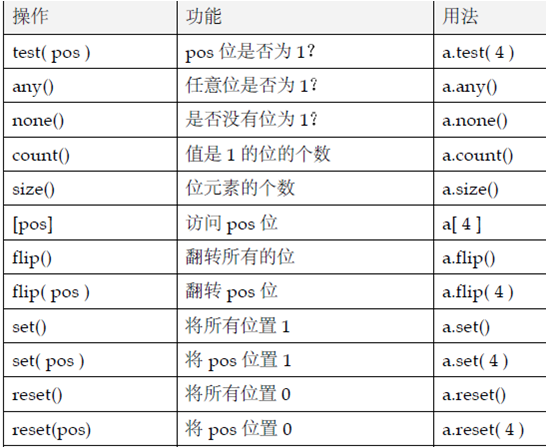
STL中的bitset
在STL中,bitset实现了相同功能。
参考: http://www.cnblogs.com/yjf512/archive/2010/11/04/1868899.html. http://www.cnblogs.com/Trony/archive/2012/09/01/2667064.html. http://www.cnblogs.com/zhanghaiba/p/3594559.html.
文章作者 Forz
上次更新 2017-06-25